
ЁОЬтФПЁПФГШеЃЌЮвБпЗРОжЭЈЙ§РзДяЗЂЯжНќКЃДІгавЛПЩвЩДЌжЛ![]() е§ЯђЙЋКЃЗНЯђааЪЛЃЌБпЗРОжбИЫйХЩГіПьЭЇ
е§ЯђЙЋКЃЗНЯђааЪЛЃЌБпЗРОжбИЫйХЩГіПьЭЇ![]() зЗИЯ(ЭМ1)ЃЎЭМ2жа
зЗИЯ(ЭМ1)ЃЎЭМ2жа![]() ЗжБ№БэЪОСНДЌЯрЖдгкКЃАЖЕФОрРы
ЗжБ№БэЪОСНДЌЯрЖдгкКЃАЖЕФОрРы![]() (КЃРя)гызЗИЯЪБМф
(КЃРя)гызЗИЯЪБМф![]() (Зж)жЎМфЕФЙиЯЕЃЎ
(Зж)жЎМфЕФЙиЯЕЃЎ
ИљОнЭМЯѓЛиД№ЮЪЬтЃК

ЃЈ1ЃЉФФвЛЬѕЯпБэЪО![]() ЕНКЃАЖЕФОрРыгызЗИЯЪБМфЕФЙиЯЕЃЛ
ЕНКЃАЖЕФОрРыгызЗИЯЪБМфЕФЙиЯЕЃЛ
ЃЈ2ЃЉЧѓГі![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉИљОнЙњМЪЙпР§ЃЌЕБ![]() ДЌааЪЛЕНРыКЃАЖ
ДЌааЪЛЕНРыКЃАЖ![]() КЃРяЕФЙЋКЃЪБЃЌНЋЮоЗЈЖдЦфНјааМьВщЃЌееДЫЫйЖШЃЌПьЭЇ
КЃРяЕФЙЋКЃЪБЃЌНЋЮоЗЈЖдЦфНјааМьВщЃЌееДЫЫйЖШЃЌПьЭЇ![]() ФмЗёдк
ФмЗёдк![]() ДЌЪЛШыЙЋКЃЧАНЋЦфРЙНиЃП
ДЌЪЛШыЙЋКЃЧАНЋЦфРЙНиЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() БэЪО
БэЪО![]() ЕНКЃАЖЕФОрРыгызЗИЯЪБМфЕФЙиЯЕЃЛЃЈ2ЃЉ
ЕНКЃАЖЕФОрРыгызЗИЯЪБМфЕФЙиЯЕЃЛЃЈ2ЃЉ![]() ЕФКЏЪ§ЙиЯЕЪНЮЊ
ЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ,
,![]() ЕФКЏЪ§ЙиЯЕЪНЮЊ
ЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЛЃЈ3ЃЉПьЭЇ
ЃЛЃЈ3ЃЉПьЭЇ![]() Фмдк
Фмдк![]() ДЌЪЛШыЙЋКЃЧАНЋЦфРЙНиЃЎ
ДЌЪЛШыЙЋКЃЧАНЋЦфРЙНиЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтКЭКЏЪ§ЭМЯѓПЩвдУїШЗФФвЛЬѕжБЯпБэЪОBЕНКЃАЖЕФОрРыгызЗИЯЪБМфЕФЙиЯЕЃЛ
ЃЈ2ЃЉИљОнКЏЪ§ЭМЯѓжаЕФЪ§ОнРћгУД§ЖЈЯЕЪ§ЗЈЧѓ![]() ЕФКЏЪ§ЙиЯЕЪНМДПЩЃЛ
ЕФКЏЪ§ЙиЯЕЪНМДПЩЃЛ
ЃЈ3ЃЉЧѓГіЯргіЕФЪБМфЃЌШЛКѓМЦЫуГіРыКЃАЖЕФОрРыМДПЩзїГіХаЖЯЃЎ
НтЃК![]() ЕБ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ОрКЃАЖ
ОрКЃАЖ![]() КЃРяЃЌМД
КЃРяЃЌМД![]() ЃЌ
ЃЌ
ЙЪ![]() БэЪО
БэЪО![]() ЕНКЃАЖЕФОрРыгызЗИЯЪБМфЕФЙиЯЕЃЛ
ЕНКЃАЖЕФОрРыгызЗИЯЪБМфЕФЙиЯЕЃЛ
![]() Щш
Щш![]() ЕФКЏЪ§ЙиЯЕЪНЮЊ
ЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЌ
ЃЌ
ДњШыЃЈ10ЃЌ5ЃЉЕУЃК![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
МД![]() ЕФКЏЪ§ЙиЯЕЪНЮЊЃК
ЕФКЏЪ§ЙиЯЕЪНЮЊЃК![]() ЃЛ
ЃЛ
Щш![]() ЕФКЏЪ§ЙиЯЕЪНЮЊ
ЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЌ
ЃЌ
гЩЭМжЊЃК![]() ЃЌ
ЃЌ
ДњШыЃЈ10ЃЌ7ЃЉЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
МД![]() ЕФКЏЪ§ЙиЯЕЪНЮЊ
ЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЛ
ЃЛ
![]() ЕБ
ЕБ![]() ЪБЃЌ
ЪБЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
вђЮЊ![]() ЃЌ
ЃЌ
ЫљвдПьЭЇ![]() Фмдк
Фмдк![]() ДЌЪЛШыЙЋКЃЧАНЋЦфРЙНиЃЎ
ДЌЪЛШыЙЋКЃЧАНЋЦфРЙНиЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧжЊЕРВЛЕШЪНЕФСНБпМгЃЈЛђМѕЃЉЭЌвЛИіЪ§ЃЈЛђЪНзгЃЉЃЌВЛЕШКХЕФЗНЯђВЛБфЃЎВЛЕШЪНзщЪЧЗёвВОпгаРрЫЦЕФаджЪФиЃПЧыНтД№ЯТСаЮЪЬтЃЎ
ЃЈ1ЃЉЭъГЩЯТСаЬюПеЃК
вбжЊ | гУЁАЃМЁБЛђЁАЃОЁБЬюПе |
| 5+2_____3+1 |
| Љ3Љ1_____Љ5Љ2 |
| 1Љ2_____4+1 |
ЃЈ2ЃЉвЛАуЕиЃЌШчЙћ![]() ФЧУДa+c_____b+dЃЈгУЁАЃМЁБЛђЁАЃОЁБЬюПеЃЉЃЎЧыФуЫЕУїЩЯЪіаджЪЕФе§ШЗадЃЎ
ФЧУДa+c_____b+dЃЈгУЁАЃМЁБЛђЁАЃОЁБЬюПеЃЉЃЎЧыФуЫЕУїЩЯЪіаджЪЕФе§ШЗадЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъжаЃЌЗДБШР§КЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§ЕуAЃЈ1ЃЌ4ЃЉЃЌBЃЈaЃЌbЃЉЃЌЦфжаaЃО1ЃЎЙ§ЕуAзїxжсДЙЯпЃЌДЙзуЮЊCЃЌЙ§ЕуBзїyжсДЙЯпЃЌДЙзуЮЊDЃЌACгыBDНЛгкЕуEЃЌСЌНгADЃЌDCЃЌCBЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§ЕуAЃЈ1ЃЌ4ЃЉЃЌBЃЈaЃЌbЃЉЃЌЦфжаaЃО1ЃЎЙ§ЕуAзїxжсДЙЯпЃЌДЙзуЮЊCЃЌЙ§ЕуBзїyжсДЙЯпЃЌДЙзуЮЊDЃЌACгыBDНЛгкЕуEЃЌСЌНгADЃЌDCЃЌCBЃЎ
ЃЈ1ЃЉЧѓkЕФжЕЃЛ
ЃЈ2ЃЉЧѓжЄЃКDCЁЮABЃЛ
ЃЈ3ЃЉЕБADЁЮBCЪБЃЌЧѓжБЯпABЕФКЏЪ§БэДяЪНЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
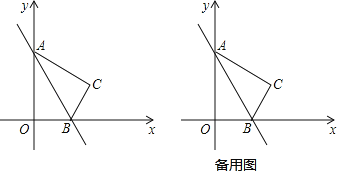
ЁОЬтФПЁПШчЭМЃЌдкзјБъЦНУцФкЃЌЕуOЪЧзјБъдЕуЃЌAЃЈ0ЃЌ6ЃЉЃЌBЃЈ2![]() ЃЌ0ЃЉЃЌЧвЁЯOBA=60ЁуЃЌНЋЁїOABбижБЯпABЗелЃЌЕУЕНЁїCABЃЌЕуOгыЕуCЖдгІЃЎ
ЃЌ0ЃЉЃЌЧвЁЯOBA=60ЁуЃЌНЋЁїOABбижБЯпABЗелЃЌЕУЕНЁїCABЃЌЕуOгыЕуCЖдгІЃЎ
ЃЈ1ЃЉЧѓЕуCЕФзјБъЃК
ЃЈ2ЃЉЖЏЕуPДгЕуOГіЗЂЃЌвд2ИіЕЅЮЛГЄЖШ/УыЕФЫйЖШбиЯпЖЮOAЯђжеЕуAдЫЖЏЃЌЩшЁїPOBЕФУцЛ§ЮЊSЃЈSЁй0ЃЉЃЌЕуPЕФдЫЖЏЪБМфЮЊtУыЃЌЧѓSгыtЕФЙиЯЕЪНЃЌВЂжБНгаДГіtЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГМвЕчЩЬГЁМЦЛЎгУ9ЭђдЊДгЩњВњГЇМвЙКНј50ЬЈЕчЪгЛњЃЌвбжЊИУГЇМвЩњВњ3жжВЛЭЌаЭКХЕФЕчЪгЛњЃЌГіГЇМлЗжБ№ЮЊAжжУПЬЈ1500дЊЃЌBжжУПЬЈ2100дЊЃЌCжжУПЬЈ2500дЊЃЎ
ЃЈ1ЃЉШєМвЕчЩЬГЁЭЌЪБЙКНјСНжжВЛЭЌаЭКХЕФЕчЪгЛњЙВ50ЬЈЃЌгУШЅ9ЭђдЊЃЌЧыФуМЦЫувЛЯТЩЬГЁгаФФМИжжНјЛѕЗНАИЃП
ЃЈ2ЃЉШєЩЬГЁЯњЪлвЛЬЈAжжЕчЪгЛњПЩЛёРћ150дЊЃЌЯњЪлвЛЬЈBжжЕчЪгЛњПЩЛёРћ200дЊЃЌЯњЪлвЛЬЈCжжЕчЪгЛњПЩЛёРћ250дЊЃЌдкЭЌЪБЙКНјСНжжВЛЭЌаЭКХЕФЕчЪгЛњЗНАИжаЃЌЮЊСЫЪЙЯњЪлЪБЛёРћзюЖрЃЌгІбЁдёФФжжЗНАИЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
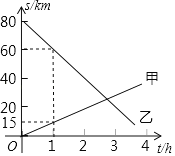
ЁОЬтФПЁПAЃЌBСНЕиЯрОр80kmЃЌМзЁЂввСНШЫЦяГЕЭЌЪБЗжБ№ДгAЃЌBСНЕиЯрЯђЖјааЃЌМйЩшЫћУЧЖМБЃГждШЫйааЪЛЃЌдђЫћУЧИїздЕНAЕиЕФОрРыs(km)ЖМЪЧЦяГЕЪБМфt(h)ЕФвЛДЮКЏЪ§ЃЌШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓввЕФsввгыtжЎМфЕФНтЮіЪНЃЛ
ЃЈ2ЃЉОЙ§ЖрГЄЪБМфМзввСНШЫЯрОр10kmЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСагЮЯЗЖдЫЋЗНЙЋЦНЕФЪЧЃЈ ЃЉ
A. ЫцвтзЊЖЏБЛЕШЗжГЩ![]() ИіЩШаЮЃЌЧвЗжБ№ОљдШЭПгаКьЁЂЛЦЁЂТЬШ§жжбеЩЋЕФзЊХЬЃЌШєжИеыжИЯђТЬЩЋЧјгђЃЌдђаЁУїЪЄЃЌЗёдђаЁССЪЄ
ИіЩШаЮЃЌЧвЗжБ№ОљдШЭПгаКьЁЂЛЦЁЂТЬШ§жжбеЩЋЕФзЊХЬЃЌШєжИеыжИЯђТЬЩЋЧјгђЃЌдђаЁУїЪЄЃЌЗёдђаЁССЪЄ
B. ДгвЛИізАга![]() ИіКьЧђЃЌ
ИіКьЧђЃЌ![]() ИіЛЦЧђКЭ
ИіЛЦЧђКЭ![]() ИіКкЧђЃЈетаЉЧђГ§беЩЋЭтЭъШЋЯрЭЌЃЉЕФДќжаШЮвтУўГівЛИіЧђЃЌШєЪЧКьЧђЃЌдђаЁУїЪЄЃЌЗёдђаЁССЪЄ
ИіКкЧђЃЈетаЉЧђГ§беЩЋЭтЭъШЋЯрЭЌЃЉЕФДќжаШЮвтУўГівЛИіЧђЃЌШєЪЧКьЧђЃЌдђаЁУїЪЄЃЌЗёдђаЁССЪЄ
C. ЭЖжРвЛУЖОљдШЕФе§ЗНЬхаЮзДЕФїЛзгЃЌШєХМЪ§ЕуГЏЩЯЃЌдђаЁУїЪЄЃЌШєЪЧЦцЪ§ЕуГЏЩЯЃЌдђаЁССЪЄ
D. ДгЗжБ№БъгаЪ§![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФЮхеХжНЬѕжаЃЌШЮвтГщШЁвЛеХЃЌШєГщЕНЕФжНЬѕЫљБъЕФЪ§зжЮЊХМЪ§ЃЌдђаЁУїЪЄЃЌШєГщЕНЕФжНЬѕЫљБъЕФЪ§зжЮЊЦцЪ§ЃЌдђаЁССЪЄ
ЕФЮхеХжНЬѕжаЃЌШЮвтГщШЁвЛеХЃЌШєГщЕНЕФжНЬѕЫљБъЕФЪ§зжЮЊХМЪ§ЃЌдђаЁУїЪЄЃЌШєГщЕНЕФжНЬѕЫљБъЕФЪ§зжЮЊЦцЪ§ЃЌдђаЁССЪЄ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
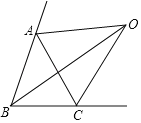
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯBACЃН70ЁуЃЌЁЯABCЕФЦНЗжЯпгыЁЯACBЕФЭтНЧЦНЗжЯпНЛгкЕуOЃЌдђЁЯBOCЃН_____ЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЁАУїЧхгАЪгГЧЁБЕФвЛЩШдВЛЁаЮУХЃЌаЁКьЕНгАЪгГЧгЮЭцЃЌЫћСЫНтЕНетЩШУХЕФЯрЙиЪ§ОнЃКетЩШдВЛЁаЮУХЫљдкЕФдВгыЫЎЦНЕиУцЪЧЯрЧаЕФЃЌAB=CD=0.25УзЃЌBD=1.5УзЃЌЧвABЃЎCDгыЫЎЦНЕиУцЖМЪЧДЙжБЕФЃЎИљОнвдЩЯЪ§ОнЃЌЧыФуАяаЁКьМЦЫуГіетЩШдВЛЁаЮУХЕФзюИпЕуРыЕиУцЕФОрРыЪЧЃЈ ЃЉ
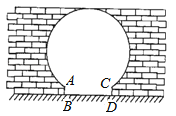
AЃЎ2Уз BЃЎ2.5Уз CЃЎ2.4Уз DЃЎ2.1Уз
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com