
【题目】已知二次函数![]() .
.
(1)求出该函数图象的顶点坐标,对称轴,图象与![]() 轴、
轴、![]() 轴的交点坐标;
轴的交点坐标;
(2)![]() 在什么范围内时,
在什么范围内时,![]() 随
随![]() 的增大而增大?当
的增大而增大?当![]() 在什么范围内时,
在什么范围内时,![]() 随
随![]() 的增大而减小?
的增大而减小?
(3)当![]() 在什么范围内时,
在什么范围内时,![]() ?
?
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
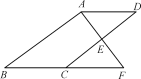
【题目】如图,E是□ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:AE=EF;
(2)若∠BAF=90°,BC=15,EF=9,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
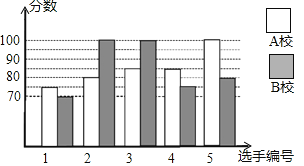
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
![]() 根据图示填写下表:
根据图示填写下表:
平均数 | 中位数 | 众数 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
![]() 结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
![]() 计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,BD是一条对角线,点P在CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QM⊥BD于M,连接AM,PM(如图1).

(1)判断AM与PM的数量关系与位置关系并加以证明;
(2)若点P在线段CD的延长线上,其它条件不变(如图2),(1)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家用电器开发公司研制出一种新型电子产品,每件的生产成本为![]() 元,按定价
元,按定价![]() 元出售,每月可销售
元出售,每月可销售![]() 万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价
万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价![]() 元,月销售量可增加
元,月销售量可增加![]() 万件.
万件.
(1)求出月销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的函数关系式(不必写
(元)之间的函数关系式(不必写![]() 的取值范围);
的取值范围);
(2)求出月销售利润![]() (万元)(利润
(万元)(利润![]() 售价-成本价)与销售单价
售价-成本价)与销售单价![]() (元)之间的函数关系式(不必写
(元)之间的函数关系式(不必写![]() 的取值范围);
的取值范围);
(3)请你通过(2)中的函数关系式及其大致图象帮助公司确定产品的销售单价范围,使月销售利润不低于![]() 万元.
万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为![]() 元的某种商品原来按每件
元的某种商品原来按每件![]() 元出售,一天可售出
元出售,一天可售出![]() 件.后来经过市场调查,发现这种商品单价每降低
件.后来经过市场调查,发现这种商品单价每降低![]() 元,其销量可增加
元,其销量可增加![]() 件.
件.
![]() 求商场经营该商品原来一天可获利润多少元?
求商场经营该商品原来一天可获利润多少元?
![]() 若商场经营该商品一天要获利润
若商场经营该商品一天要获利润![]() 元,并让顾客得到实惠,则每件商品应降价多少元?
元,并让顾客得到实惠,则每件商品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
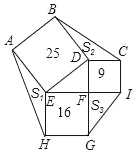
【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
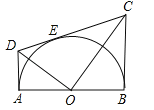
【题目】如图,AB为半圆O的在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③![]() ,④OD:OC=DE:EC,⑤
,④OD:OC=DE:EC,⑤![]() ,正确的有( )
,正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com