
【题目】将纸片△ABC沿DE折叠使点A落在A′处的位置.
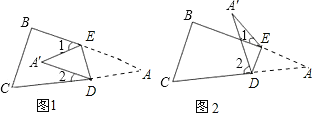
(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.
(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是 .
(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.
【答案】(1)2∠A=∠1+∠2,理由见解析;(2)2∠A=∠2;(3)2∠A=∠2﹣∠1,理由见解析.
【解析】
试题分析:(1)根据折叠性质得出∠AED=∠A′ED,∠ADE=∠A′DE,根据三角形内角和定理得出∠AED+∠ADE=180°﹣∠A,代入∠1+∠2=180°+180°﹣2(∠AED+∠ADE)求出即可;
(2)根据三角形外角性质得出∠DME=∠A′+∠1,∠2=∠A+∠DME,代入即可求出答案.
解:(1)图1中,2∠A=∠1+∠2,
理由是:∵延DE折叠A和A′重合,
∴∠AED=∠A′ED,∠ADE=∠A′DE,
∵∠AED+∠ADE=180°﹣∠A,∠1+∠2=180°+180°﹣2(∠AED+∠ADE),
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A;
(2)2∠A=∠2,如图

∠2=∠A+∠EA′D=2∠A,
故答案为:2∠A=∠2;
(3)如图2,2∠A=∠2﹣∠1,
理由是:∵延DE折叠A和A′重合,

∴∠A=∠A′,
∵∠DME=∠A′+∠1,∠2=∠A+∠DME,
∴∠2=∠A+∠A′+∠1,
即2∠A=∠2﹣∠1.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.

(1)点M(3,2) 和谐点(填“是”或“不是”);
(2)若点P(a,6)是和谐点,a的值为 ;
(3)若(2)中和谐点P(a,6)在y=﹣4x+m上,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
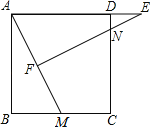
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面直角坐标系内,将函数y=2x2+4x﹣3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是( )
A.(﹣3,﹣6) B.(1,﹣4)
C.(1,﹣6) D.(﹣3,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正方体的六个面上分别标有﹣1,﹣2,﹣3,﹣4,﹣5,﹣6中的一个数,各个面上所标数字都不相同,如图是这个正方体的三种放置方法,三个正方体下底面所标数字分别是a,b,c,则a+b+c+abc= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,DC∥AB,AD=BC,BD平分∠ABC.

(1)求证:AD=DC;
(2)如图2,在上述条件下,若∠A=∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.判断△DEF的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.
如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若(![]() ☆3)☆(﹣
☆3)☆(﹣![]() )=8,求a的值;
)=8,求a的值;
(3)若2☆x=m,(![]() x)☆3=n(其中x为有理数),试比较m,n的大小.
x)☆3=n(其中x为有理数),试比较m,n的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com