
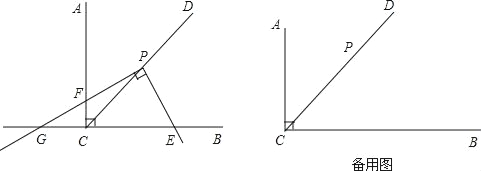
【题目】已知,∠ACB=90°,CD是∠ACB的平分线,点P在CD上,CP=![]() .将三角板的直角顶点放置在点P处,绕着点P旋转,三角板的一条直角边与射线CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.
.将三角板的直角顶点放置在点P处,绕着点P旋转,三角板的一条直角边与射线CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.
(1)如图,当点F在射线CA上时,
①求证:PF=PE.
②设CF=x,EG=y,求y与x的函数解析式并写出函数的定义域.
(2)连接EF,当△CEF与△EGP相似时,求EG的长.
【答案】(1)①见解析,②![]() (0≤x<1);(2)当△CEF与△EGP相似时,①当点F在射线CA上时,EG=2
(0≤x<1);(2)当△CEF与△EGP相似时,①当点F在射线CA上时,EG=2![]() ,②当点F在AC延长线上时,EG=2
,②当点F在AC延长线上时,EG=2![]() .
.
【解析】
(1)①过点P作PM⊥AC,PN⊥BC,垂足分别为M、N,由已知条件证明△PMF≌△PNE即可证明PF=PE;②利用①中的三角形全等和相似三角形的性质即可求出y与x的函数解析式,再写出其自变量的取值范围即可;
(2)当△CEF与△EGP相似时,点F的位置有两种情况:①当点F在射线CA上时,②当点F在AC延长线上时,分别讨论求出满足题意的EG长即可.
(1)①过点P作PM⊥AC,PN⊥BC,垂足分别为M、N,
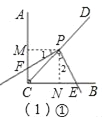
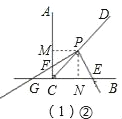
∵CD是∠ACB的平分线,
∴PM=PN,
由∠PMC=∠MCN=∠CNP=90°,得∠MPN=90°,
∴∠1+∠FPN=90°,
∵∠2+∠FPN=90°,
∴∠1=∠2,
∴△PMF≌△PNE,
∴PF=PE;
②∵CP=![]() ,
,
∴CN=CM=1.
∵△PMF≌△PNE,
∴NE=MF=1﹣x.
∴CE=2﹣x.
∵CF∥PN,
∴△GCF∽△GNP,
∴![]() .
.
∴![]() .
.
∴![]() (0≤x<1).
(0≤x<1).
(2)当△CEF与△EGP相似时,点F的位置有两种情况:
①当点F在射线CA上时,
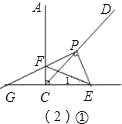
∵∠GPE=∠FCE=90°,∠1≠∠PEG,
∴∠G=∠1.
∴FG=FE.
∴CG=CE.
在Rt△EGP中,EG=2CP=2![]() ;
;
②当点F在AC延长线上时,
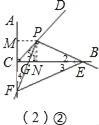
∵∠GPE=∠FCE=90°,∠1≠∠2,
∴∠3=∠2,
∵∠1=45°+∠5,∠1=45°+∠2,
∴∠5=∠2,
易证∠3=∠4,可得∠5=∠4,
∴FC=CP=![]() ,
,
∴FM=1+![]() ,
,
易证△PMF≌△PNE,
可得EN=1+![]() ,
,
∵CF∥PN,
![]() ,
,
∴GN=![]() ﹣1.
﹣1.
∴EG=2![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)问题发现与探究:
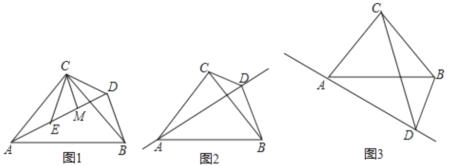
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM⊥AE于点M,连接BD,则①线段AE、BD之间的大小关系是 ,∠ADB= °;②求证:AD=2CM+BD.
(2)问题拓展与应用:
如图2、图3,等腰Rt△ABC中,∠ACB=90°,过点A作直线,在直线上取点D,∠ADC=45°,连结BD,BD=1,AC=![]() ,则点C到直线AD的距离是 .(直接写出答案)
,则点C到直线AD的距离是 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5 ![]() 米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
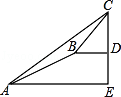
A. 7米 B. 7.2米 C. 9.7米 D. 15.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造![]() 两种型号的沼气池共20个,以解决该村所有农户的燃料问题,两种型号沼气池的占地面积、使用农户数及造价见下表:
两种型号的沼气池共20个,以解决该村所有农户的燃料问题,两种型号沼气池的占地面积、使用农户数及造价见下表:
型号 | 占地面积( | 使用农户数(户/个) | 造价(万元/个) |
|
|
|
|
|
|
|
|
已知可供建造沼气池的占地面积不超过![]() ,该村农户共有492户.
,该村农户共有492户.
(1)满足条件的方案共有几种?写出解答过程;
(2)通过计算判断,哪种建造方案最省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
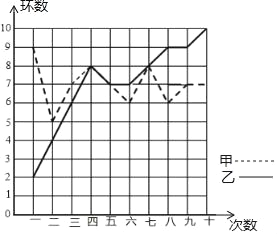
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中不正确的是( )
A.抛掷一枚硬币,硬币落地时正面朝上是随机事件
B.把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件
C.一个盒子中有白球![]() 个,红球6个,黑球
个,红球6个,黑球![]() 个(每个球除了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么
个(每个球除了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么![]() 与
与![]() 的和是6
的和是6
D.任意打开七年级下册数学教科书,正好是100页是确定事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
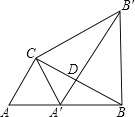
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,连接BB′,求BB′的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2,若y1≠y2,取y1和y2中较小值为M;若y1=y2,记M=y1=y2.①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是_____(填写所有正确结论的序号).
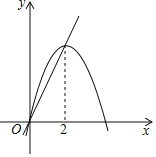
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com