
【题目】这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5 ![]() 米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
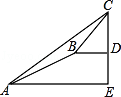
A. 7米 B. 7.2米 C. 9.7米 D. 15.5米
【答案】A
【解析】
作BF⊥AE于F,则FE=BD=6米,DE=BF,设BF=x米,则AF=2x米,在Rt△ABF中,由勾股定理得出方程,解方程求出DE=BF=5米,AF=10米,得出AE的长度,在Rt△ACE中,由三角函数求出CE,计算即可.
作BF⊥AE于F,

则FE=BD=6米,DE=BF,
∵斜面AB的坡度i=1:2,
∴AF=2BF,
设BF=x米,则AF=2x米,
在Rt△ABF中,由勾股定理得:x2+(2x)2=(5![]() )2,
)2,
解得:x=5,
∴DE=BF=5米,AF=10米,
∴AE=AF+FE=16米,
在Rt△ACE中,CE=AEtan37°≈16×0.75=12米,
∴CD=CE-DE=12米-5米=7米,
故选:A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
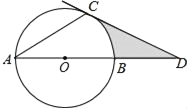
【题目】如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,且∠A=∠D.
(1)求∠ACD的度数;
(2)若CD=3,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为_______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD,DEFG都是正方形,边长分别为m,n(m<n).坐标原点O为AD的中点,A,D,E在y轴上,若二次函数y=ax2的图象过C,F两点,则![]() =( )
=( )

A.![]() +1B.
+1B.![]() +1C.2
+1C.2![]() ﹣1D.2
﹣1D.2![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
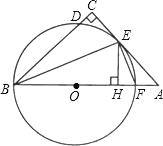
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EH=3,求BF及AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
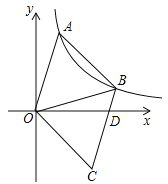
【题目】(2017江苏省连云港市)如图,已知等边三角形OAB与反比例函数![]() (k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则
(k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则![]() 的值为____.(已知sin15°=
的值为____.(已知sin15°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
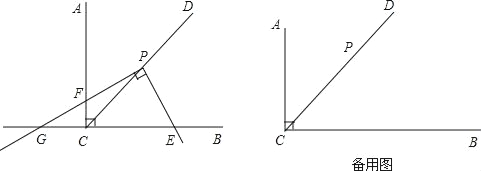
【题目】已知,∠ACB=90°,CD是∠ACB的平分线,点P在CD上,CP=![]() .将三角板的直角顶点放置在点P处,绕着点P旋转,三角板的一条直角边与射线CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.
.将三角板的直角顶点放置在点P处,绕着点P旋转,三角板的一条直角边与射线CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.
(1)如图,当点F在射线CA上时,
①求证:PF=PE.
②设CF=x,EG=y,求y与x的函数解析式并写出函数的定义域.
(2)连接EF,当△CEF与△EGP相似时,求EG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两堆背面完全相同的扑克,第一堆正面分别写有数字1、2、3、4,第二堆正面分别写有数字1、2、3.分别混合后,小玲从第一堆中随机抽取一张,把卡片上的数字作为被减数;小惠从第二堆中随机抽取一张,把卡片上的数字作为减数,然后计算出这两个数的差.
(1)请用画树状图或列表的方法,求这两数差为0的概率;
(2)小玲与小惠作游戏,规则是:若这两数的差为非负数,则小玲胜;否则,小惠胜.你认为该游戏规则公平吗?如果公平,请说明理由.如果不公平,请你修改游戏规则,使游戏公平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com