
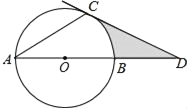
【题目】如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,且∠A=∠D.
(1)求∠ACD的度数;
(2)若CD=3,求图中阴影部分的面积.
【答案】(1) ∠ACD=120°;(2)![]()
【解析】
(1)连接OC,由过点C的切线交AB的延长线于点D,推出OC⊥CD,推出∠OCD=90°,即∠D+∠COD=90°,由AO=CO,推出∠A=∠ACO,推出∠COD=2∠A,可得3∠D=90°,推出∠D=30°,即可解决问题
(2)先求△OCD和扇形OCB的面积,进而可求出图中阴影部分的面积.
解:(1)连接OC,

∵过点C的切线交AB的延长线于点D,
∴OC⊥CD,
∴∠OCD=90°,
即∠D+∠COD=90°,
∵AO=CO,
∴∠A=∠ACO,
∴∠COD=2∠A,
∵∠A=∠D,
∴∠COD=2∠D,
∴3∠D=90°,
∴∠D=30°,
∴∠ACD=180°﹣∠A﹣∠D=180°﹣30°﹣30°=120°.
(2)由(1)可知∠COD=60°
在Rt△COD中,∵CD=3,
∴OC=3×![]()
= ![]() ,
,
∴阴影部分的面积=![]()


科目:初中数学 来源: 题型:
【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,根据图形可知他得出的这个推论指( )

A. S矩形ABMN=S矩形MNDCB. S矩形EBMF=S矩形AEFN
C. S矩形AEFN=S矩形MNDCD. S矩形EBMF=S矩形NFGD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度)
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于原点对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出线段OB旋转到OB2扫过图形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
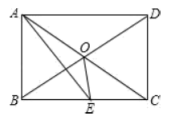
【题目】如图所示,矩形ABCD中,AE平分![]() 交BC于E,
交BC于E,![]() ,则下面的结论:①
,则下面的结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论有( )
,其中正确结论有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
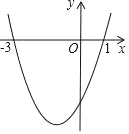
【题目】如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为﹣3,1,则下列结论正确的个数有( )①ac>0;②2a﹣b=0;③4a﹣2b+c>0;④对于任意实数m均有am2+bm≥a﹣b.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,数学老师出示了如下题目:
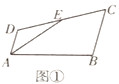
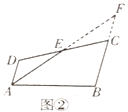
如图①,在四边形![]() 中,
中,![]() 是边
是边![]() 的中点,
的中点,![]() 是
是![]() 的平分线,
的平分线,![]() .
.
求证:![]() .
.
小聪同学发现以下两种方法:
方法1:如图②,延长![]() 、
、![]() 交于点
交于点![]() .
.
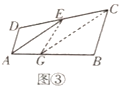
方法2:如图③,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() .
.
(1)请你任选一种方法写出这道题的完整的证明过程;
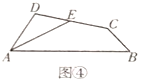
(2)如图④,在四边形![]() 中,
中,![]() 是
是![]() 的平分线,
的平分线,![]() 是边
是边![]() 的中点,
的中点,![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②![]() >0;③ac﹣b+1=0;④OAOB=﹣
>0;③ac﹣b+1=0;④OAOB=﹣![]() .
.
其中正确结论的个数是( )

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现与探究:
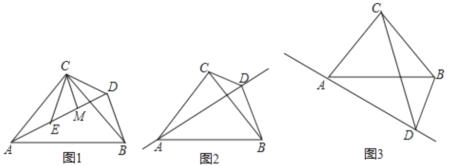
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM⊥AE于点M,连接BD,则①线段AE、BD之间的大小关系是 ,∠ADB= °;②求证:AD=2CM+BD.
(2)问题拓展与应用:
如图2、图3,等腰Rt△ABC中,∠ACB=90°,过点A作直线,在直线上取点D,∠ADC=45°,连结BD,BD=1,AC=![]() ,则点C到直线AD的距离是 .(直接写出答案)
,则点C到直线AD的距离是 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
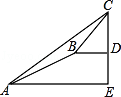
【题目】这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5 ![]() 米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
A. 7米 B. 7.2米 C. 9.7米 D. 15.5米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com