
【题目】(1)问题发现与探究:
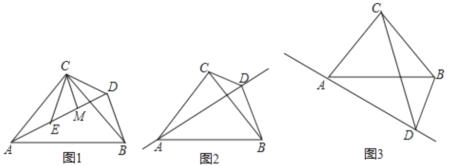
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM⊥AE于点M,连接BD,则①线段AE、BD之间的大小关系是 ,∠ADB= °;②求证:AD=2CM+BD.
(2)问题拓展与应用:
如图2、图3,等腰Rt△ABC中,∠ACB=90°,过点A作直线,在直线上取点D,∠ADC=45°,连结BD,BD=1,AC=![]() ,则点C到直线AD的距离是 .(直接写出答案)
,则点C到直线AD的距离是 .(直接写出答案)
【答案】(1)① AE=BD,90;②见解析;(2)![]() 或
或![]()
【解析】
(1)根据等腰直角三角形的性质得到AC=BC,CE=CD,由∠ACB=∠DCE=90°,得到∠ACE=∠BCD,证得△ACD≌△BCE,根据全等三角形的性质得到AE=BD,∠AEC=∠BDC,根据邻补角的定义得到∠AEC=135°即可得到结论;②根据等腰直角三角形的性质即可得到结论.
(2)如图2,过C作CH⊥AD于H,CE⊥CD交AD于E,于是得到△CDE是等腰直角三角形,由(1)知,AE=BD=1,∠ADB=90°,根据勾股定理得到AB=![]() =2,
=2,![]()
,由等腰直角三角形的性质即可得到结论.如图3,过C作CH⊥AD于H,CE⊥CD交DA的延长线于E,于是得到△CDE是等腰直角三角形,由(1)知,AE=BD=1,∠ADB=90°,根据勾股定理得到AB=![]() =2,
=2,![]() ,于是可得DE的长度,利用等腰直角三角形DEC的性质得出结论.
,于是可得DE的长度,利用等腰直角三角形DEC的性质得出结论.
解:(1)①∵△ACB和△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,
∵∠ACB=∠DCE=90°,
∴∠ACE=∠BCD,
在△ACE与△BCD中,
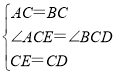 ,
,
∴△ACE≌△BCD,
∴AE=BD,∠AEC=∠BDC,
∵∠CED=∠CDE=45°,
∴∠AEC=135°,∴∠BDC=135°,
∴∠ADB=90°;
故答案为:AE=BD,90°;
②在等腰直角三角形DCE中,CM为斜边DE上的高,
∴CM=DM=ME,∴DE=2CM.
∴![]()
(2) 如图2,过C作CH⊥AD于H,CE⊥CD交AD于E,又∠ADC=45°

则△CDE是等腰直角三角形,
由(1)知,AE=BD=1,∠ADB=90°,
∵AB=![]() =2,
=2,
∴AD=![]() ,
,
∴DE=AD-AE=![]() ,
,
∵△CDE是等腰直角三角形,
∴CH=![]() DE=
DE=![]() ,
,
如图3所示,过C作CH⊥AD于H,CE⊥CD交DA的延长线于E,又∠ADC=45°
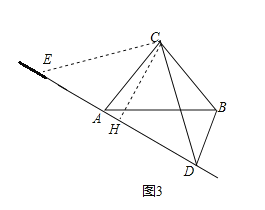
则△CDE是等腰直角三角形,由(1)知,AE=BD=1,∠ADB=90°,
∵AB=![]() =2, ∴AD=
=2, ∴AD= ![]() ,
,
∴DE=AE+AD=1+![]() ,
,
∵△CDE是等腰直角三角形,
∴CH=![]() DE=
DE=![]() ,
,
∴点C到直线的距离是 ![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
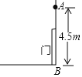
【题目】如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移至该灯5m及5m内,灯就会自动发光,小明身高1.5m,他走到离墙_______的地方灯刚好发光.
查看答案和解析>>
科目:初中数学 来源: 题型:
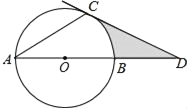
【题目】如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,且∠A=∠D.
(1)求∠ACD的度数;
(2)若CD=3,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,则此一次函数的解析式为__________,△AOC的面积为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用我们学过的知识,可以导出下面这个等式:
![]() .
.
该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
(1)请你展开右边检验这个等式的正确性;
(2)利用上面的式子计算:
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为_______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD,DEFG都是正方形,边长分别为m,n(m<n).坐标原点O为AD的中点,A,D,E在y轴上,若二次函数y=ax2的图象过C,F两点,则![]() =( )
=( )

A.![]() +1B.
+1B.![]() +1C.2
+1C.2![]() ﹣1D.2
﹣1D.2![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
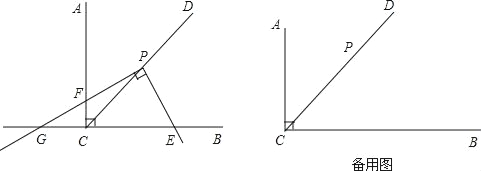
【题目】已知,∠ACB=90°,CD是∠ACB的平分线,点P在CD上,CP=![]() .将三角板的直角顶点放置在点P处,绕着点P旋转,三角板的一条直角边与射线CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.
.将三角板的直角顶点放置在点P处,绕着点P旋转,三角板的一条直角边与射线CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.
(1)如图,当点F在射线CA上时,
①求证:PF=PE.
②设CF=x,EG=y,求y与x的函数解析式并写出函数的定义域.
(2)连接EF,当△CEF与△EGP相似时,求EG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com