
【题目】如图,ABCD,DEFG都是正方形,边长分别为m,n(m<n).坐标原点O为AD的中点,A,D,E在y轴上,若二次函数y=ax2的图象过C,F两点,则![]() =( )
=( )

A.![]() +1B.
+1B.![]() +1C.2
+1C.2![]() ﹣1D.2
﹣1D.2![]() ﹣1
﹣1
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AE平分![]() 交BC于E,
交BC于E,![]() ,则下面的结论:①
,则下面的结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论有( )
,其中正确结论有( )
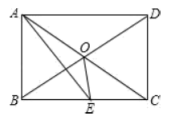
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现与探究:
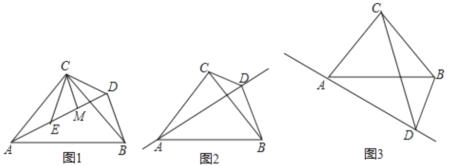
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM⊥AE于点M,连接BD,则①线段AE、BD之间的大小关系是 ,∠ADB= °;②求证:AD=2CM+BD.
(2)问题拓展与应用:
如图2、图3,等腰Rt△ABC中,∠ACB=90°,过点A作直线,在直线上取点D,∠ADC=45°,连结BD,BD=1,AC=![]() ,则点C到直线AD的距离是 .(直接写出答案)
,则点C到直线AD的距离是 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,弦CD⊥AB于点E,G是![]() 上一动点,AG,DC的延长线交于点F,连结BC.
上一动点,AG,DC的延长线交于点F,连结BC.
(1)若AB=4,∠B=60°,求![]() 的长;
的长;
(2)设∠DGF=![]() °,∠BCD=
°,∠BCD=![]() °,求
°,求![]() 关于
关于![]() 的函数表达式.
的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
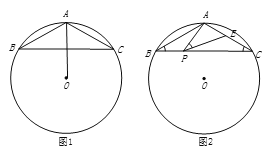
【题目】如图,等腰△ABC内接于半径为5的⊙O,AB=AC,BC=8.
(1)如图1,连结OA.
①求证:OA⊥BC;
②求腰AB的长.
(2)如图2,点P是边BC上的动点(不与点B,C重合),∠APE=∠B=∠C,PE交AC于E.
①求线段CE的最大值;
②当AP=PC时,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
(1)试确定该抛物线的对称轴及当![]() 时对应的函数值;
时对应的函数值;
(2)试确定抛物线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
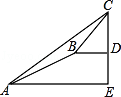
【题目】这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5 ![]() 米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
A. 7米 B. 7.2米 C. 9.7米 D. 15.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造![]() 两种型号的沼气池共20个,以解决该村所有农户的燃料问题,两种型号沼气池的占地面积、使用农户数及造价见下表:
两种型号的沼气池共20个,以解决该村所有农户的燃料问题,两种型号沼气池的占地面积、使用农户数及造价见下表:
型号 | 占地面积( | 使用农户数(户/个) | 造价(万元/个) |
|
|
|
|
|
|
|
|
已知可供建造沼气池的占地面积不超过![]() ,该村农户共有492户.
,该村农户共有492户.
(1)满足条件的方案共有几种?写出解答过程;
(2)通过计算判断,哪种建造方案最省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
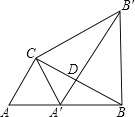
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,连接BB′,求BB′的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com