
【题目】如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为_______

【答案】![]()
【解析】
如图取CD的中点F,连接BF延长BF交AD的延长线于G,作FH⊥AB于H,EK⊥AB于K.作BT⊥AD于T.由△BCF≌△GDF,推出BC=DG,BF=FG,由△FBC≌△FBH,△FAH≌△FAD,推出BC=BH,AD=AH,由题意AD=DC=4,设BC=TD=BH=x,在Rt△ABT中,∵AB2=BT2+AT2,可得(x+4)2=42+(4-x)2,推出x=1,推出BC=BH=TD=1,AB=5,设AK=EK=y,DE=z,根据AE2=AK2+EK2=AD2+DE2,BE2=BK2+KE2=BC2+EC2,可得42+z2=2y2①,(5-y)2+y2=12+(4-z)2 ②,由此求出y即可解决问题.
解:如图取CD的中点F,连接BF延长BF交AD的延长线于G,作FH⊥AB于H,EK⊥AB于K.作BT⊥AD于T.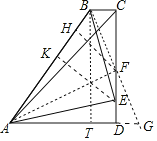
∵BC∥AG,
∴∠BCF=∠FDG,
∵∠BFC=∠DFG,FC=DF,
∴△BCF≌△GDF,
∴BC=DG,BF=FG,
∵AB=BC+AD,AG=AD+DG=AD+BC,
∴AB=AG,∵BF=FG,
∴BF⊥AF,∠ABF=∠G=∠CBF,
∵FH⊥BA,FC⊥BC,
∴FH=FC,易证△FBC≌△FBH,△FAH≌△FAD,
∴BC=BH,AD=AH,
由题意AD=DC=4,设BC=TD=BH=x,
在Rt△ABT中,∵AB2=BT2+AT2,
∴(x+4)2=42+(4-x)2,
∴x=1,
∴BC=BH=TD=1,AB=5,
设AK=EK=y,DE=z,
∵AE2=AK2+EK2=AD2+DE2,BE2=BK2+KE2=BC2+EC2,
∴42+z2=2y2 ①,
(5-y)2+y2=12+(4-z)2 ②
由②得到25-10y+2y2=5-8z+z2 ③,
①代入③可得z=![]() ④
④
④代入①可得y=![]() (负根已经舍弃),
(负根已经舍弃),
∴S△ABE=![]() ×5×
×5×![]() =
=![]() ,
,
故答案为:![]()


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度)
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于原点对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出线段OB旋转到OB2扫过图形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②![]() >0;③ac﹣b+1=0;④OAOB=﹣
>0;③ac﹣b+1=0;④OAOB=﹣![]() .
.
其中正确结论的个数是( )

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现与探究:
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM⊥AE于点M,连接BD,则①线段AE、BD之间的大小关系是 ,∠ADB= °;②求证:AD=2CM+BD.
(2)问题拓展与应用:
如图2、图3,等腰Rt△ABC中,∠ACB=90°,过点A作直线,在直线上取点D,∠ADC=45°,连结BD,BD=1,AC=![]() ,则点C到直线AD的距离是 .(直接写出答案)
,则点C到直线AD的距离是 .(直接写出答案)
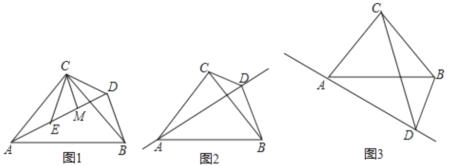
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】质地均匀的骰子六个面分别刻有1到6的点数,扔两次骰子,得到向上一面的两个点数,则下列事件中,是必然事件的是( )
A. 点数都是偶数 B. 点数的和为奇数
C. 点数的和小于13 D. 点数的和小于2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,弦CD⊥AB于点E,G是![]() 上一动点,AG,DC的延长线交于点F,连结BC.
上一动点,AG,DC的延长线交于点F,连结BC.
(1)若AB=4,∠B=60°,求![]() 的长;
的长;
(2)设∠DGF=![]() °,∠BCD=
°,∠BCD=![]() °,求
°,求![]() 关于
关于![]() 的函数表达式.
的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC内接于半径为5的⊙O,AB=AC,BC=8.
(1)如图1,连结OA.
①求证:OA⊥BC;
②求腰AB的长.
(2)如图2,点P是边BC上的动点(不与点B,C重合),∠APE=∠B=∠C,PE交AC于E.
①求线段CE的最大值;
②当AP=PC时,求BP的长.
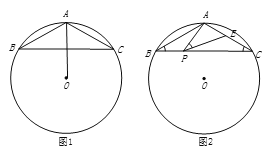
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5 ![]() 米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
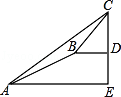
A. 7米 B. 7.2米 C. 9.7米 D. 15.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com