
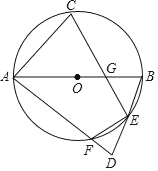
【题目】如图,AB是⊙O的直径,点C是弧AB的中点,点D是⊙O外一点,AD=AB,AD交⊙O于F,BD交⊙O于E,连接CE交AB于G.
(1)证明:∠C=∠D;
(2)若∠BEF=140°,求∠C的度数;
(3)若EF=2,tanB=3,求CECG的值.
【答案】(1)见解析;(2)70°;(3)20.
【解析】
(1)先根据等边对等角得出∠B=∠D,即可得出结论;
(2)先判断出∠DFE=∠B,进而得出∠D=∠DFE,即可求出∠D=70°,即可得出结论;
(3)先求出BE=EF=2,进而求AE=6,即可得出AB,进而求出AC,再判断出△ACG∽△ECA,即可得出结论.
(1)∵AB=AD,
∴∠B=∠D,
∵∠B=∠C,
∴∠C=∠D;
(2)∵四边形ABEF是圆内接四边形,
∴∠DFE=∠B,
由(1)知,∠B=∠D,
∴∠D=∠DFE,
∵∠BEF=140°=∠D+∠DFE=2∠D,
∴∠D=70°,
由(1)知,∠C=∠D,
∴∠C=70°;
(3)如图,由(2)知,∠D=∠DFE,
∴EF=DE,
连接AE,OC,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴BE=DE,
∴BE=EF=2,
在Rt△ABE中,tanB=![]() =3,
=3,
∴AE=3BE=6,根据勾股定理得,AB=![]() ,
,
∴OA=OC=![]() AB=
AB=![]() ,
,
∵点C是![]() 的中点,
的中点,
∴![]() ,
,
∴∠AOC=90°,
∴AC=![]() OA=2
OA=2![]() ,
,
∵![]() ,
,
∴∠CAG=∠CEA,
∵∠ACG=∠ECA,
∴△ACG∽△ECA,
∴![]() ,
,
∴CECG=AC2=20.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )

A.一处B.二处C.三处D.四处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以水![]() 润
润![]() 城,打造
城,打造![]() 四河一库
四河一库![]() 生态水系工程,是巩义坚持不懈推进文明创建与百城提质深度融合的缩影,伊洛河畔正是此项目中的一段.如今,伊洛河畔需要铺设一条长为
生态水系工程,是巩义坚持不懈推进文明创建与百城提质深度融合的缩影,伊洛河畔正是此项目中的一段.如今,伊洛河畔需要铺设一条长为![]() 米的管道,决定由甲、乙两个工程队来完成.已知甲工程队比乙工程队每天能多铺设
米的管道,决定由甲、乙两个工程队来完成.已知甲工程队比乙工程队每天能多铺设![]() 米,且甲工程队铺设
米,且甲工程队铺设![]() 米所用的天数与乙工程队铺设
米所用的天数与乙工程队铺设![]() 米所用的天数相同.(完成任务的工期为整数)
米所用的天数相同.(完成任务的工期为整数)
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项管道铺设任务的工期不超过![]() 天,那么为两工程队分配工程量的方案有几种?请你帮助设计出来(工程队分配工程量为整百数)
天,那么为两工程队分配工程量的方案有几种?请你帮助设计出来(工程队分配工程量为整百数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD,AC分别是⊙O的直径和弦.且∠CAD=30°.OB⊥AD交AC于点B.若OB=4,则BC长为( )
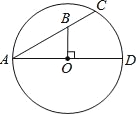
A. 2 B. 3 C. 3.6 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
关于x的方程:x+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() ;x﹣
;x﹣![]() =c﹣
=c﹣![]() (可变形为x+
(可变形为x+![]() =c+
=c+![]() )的解为x1=c,x2=
)的解为x1=c,x2=![]() ;x+
;x+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() Zx+
Zx+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() Z.
Z.
(1)归纳结论:根据上述方程与解的特征,得到关于x的方程x+![]() =c+
=c+![]() (m≠0)的解为 .
(m≠0)的解为 .
(2)应用结论:解关于y的方程y﹣a=![]() ﹣
﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
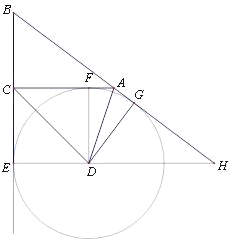
【题目】如图,在△ABC中,BC=a,AC=b,AB=c,⊙D与BC、AC、AB都相切,切点分别是E、F、G,BA、ED的延长线交于点H,a、b是关于x的方程x2﹣(c+4)x+4c+8=0的两个根.
(1)求证:△ABC是直角三角形;
(2)若25asin∠BAC=9c,求四边形CEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元。2016年投入教育经费8640万元。假设该县这两年投入教育经费的年平均增长率相同。
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com