
【题目】如图所示,A,B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午2时骑摩托车按同路从A地出发驶往B地,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午行驶的时间t之间的关系.根据图象回答下列问题: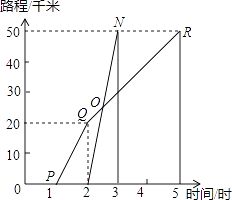
(1)甲在该日下午2﹣5时骑自行车的速度是多少?
(2)乙从出发大约用多长时间就能追上甲?
(3)甲骑自行车和乙骑摩托车在全程的平均速度分别是多少?
【答案】
(1)解:甲在该日下午2﹣5时骑自行车的速度是 ![]() =10千米/小时
=10千米/小时
(2)解:由图可知:M(2,0),N(3,50),Q(2,20),R(5,50)
设直线QR的函数表达式为y1=k1x+b1,
将Q(2,20),R(5,50)代入得:
![]() ,
,
解得 ![]() ,
,
设直线MN的函数表达式为y2=k2x+b2,
将M(2,0),N(3,50)代入得:
![]() ,
,
解得 ![]() ,
,
则y1=10x,y2=50x﹣100,
联立两式可得直线QR、MN的交点的坐标为(2.5,25).
所以乙出发半小时后追上甲
(3)解:乙的平均速度为 ![]() =50千米/时,甲的平均速度为
=50千米/时,甲的平均速度为 ![]() =12.5千米/时
=12.5千米/时
【解析】(1)根据速度=路程÷时间即可解决问题;
(2)先求得两函数的解析式,然后再组成方程组,求得两个函数交点的坐标即可;
(3)用各自的总路程÷各自的总时间,列式计算即可求解.


科目:初中数学 来源: 题型:
【题目】三角形的三边长分别为①5,12,13; ②9,40,41; ③8,15,17; ④13,84,85. 其中能够构成直角三角形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4) ![]() 中正确的有( )
中正确的有( )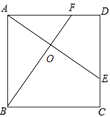
A. 4个
B. 3个
C. 2个
D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:①AD=DC;②AB=BD;③AB=![]() BC;④BD=CD,
BC;④BD=CD,
其中正确的个数为( )
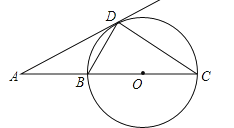
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45°角)如图放置,使直角顶点C重合,若DE∥BC,则∠1的度数是( )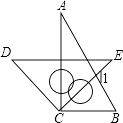
A.75°
B.105°
C.110°
D.120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com