练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】三角形的三边长分别为①5,12,13; ②9,40,41; ③8,15,17; ④13,84,85. 其中能够构成直角三角形的有（ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    【答案】D

    【解析】试题解析：①、∵52+122=169=132，∴能构成直角三角形，故本小题正确；

    ②、92+402=1681=412=169，∴能构成直角三角形，故本小题正确；

    ③、82+152=289=172，∴能构成直角三角形，故本小题正确；

    ④、∵152+202=625=152=49，∴能构成直角三角形，故本小题正确．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图的七边形ABCDEFG中，AB、ED的延长线相交于O点．若图中∠1、∠2、∠3、∠4的外角的角度和为220°，则∠BOD的度数为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算下列各式：
    （1）（﹣2）0+（ ）﹣2﹣（﹣0.5）201622017
    （2）先化简，再求值：（a+b）（a﹣b）+（a+b）2﹣2a2 ， 其中a=2017，b=﹣ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，点O为直线BD上的一点，OC⊥OA，垂足为点O，∠COD=2∠BOC，求∠AOB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商品原价200元，连续两次降价a%后售价为148元，下列所列方程正确的是（ ）
    A.200（1+a%）2=148
    B.200（1﹣a%）2=148
    C.200（1﹣2a%）=148
    D.200（1﹣a2%）=148

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，A，B两地相距50千米，甲于某日下午1时骑自行车从A地出发驶往B地，乙也于同日下午2时骑摩托车按同路从A地出发驶往B地，图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午行驶的时间t之间的关系．根据图象回答下列问题：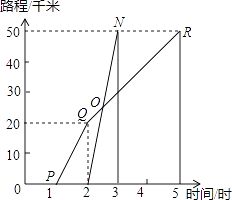

    （1）甲在该日下午2﹣5时骑自行车的速度是多少？
    （2）乙从出发大约用多长时间就能追上甲？
    （3）甲骑自行车和乙骑摩托车在全程的平均速度分别是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=50°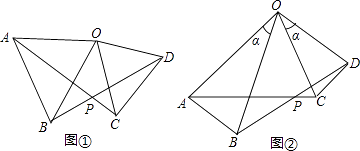
    （1）求证：①AC=BD；②∠APB=50°；
    （2）如图②，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系为 ， ∠APB的大小为

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解不等式： 并在数轴上表示出它的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道有两条边相等的三角形叫做等腰三角形．类似的，我们定义：至少有一组对边相等的四边形叫做等对边四边形．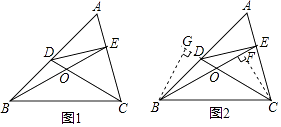

    （1）请写出一个你学过的四边形中是等对边四边形的图形的名称．
    （2）如图1，在△ABC中，点D、E分别在AB、AC上，且CD、BE相交于点O，若∠A=60°，∠DCB=∠EBC= ∠A．请你写出与∠A相等的角．
    （3）我们易证图中的四边形BCED是等对边四边形．
    （提示：如图2，可证△BGO≌△CFO再证△BGD≌△CFE，可得到结论BD=CE．不需证明）
    若在△ABC中，如果∠A是不等于60°的锐角，D、E分别在AB、AC上，且CD、BE相交于点O，∠DCB=∠EBC= ∠A．探究：满足上述条件的图形中是否存在等对边四边形，并证明你的结论．

    查看答案和解析>>

    同步练习册答案