Question

17．（1）[问题发现]
已知：△ABC和△ADE都是等腰直角三角形，∠CAB=∠EAD=90°，连接CE，BD，猜想线段CE，BD的数量关系为CE=BD；

（2）[问题研究]
如图2，△ABC和△ADE都是等腰直角三角形，∠CAB=∠EAD=90°，点E，D，B在同一条直线上，AM为△ADE斜边上的高，连接CE，请判断CE，AM，BE之间的数量关系，并说明理由；
（3）[问题解决]
如图3，在正方形ABCD中，AB=5，若在同一平面内的点P满足PD=2，且∠BPD=90°，请求出△ABP的面积．

Answer 1

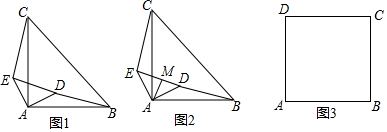
分析 （1）CE=BD，证明△AEC≌△ADB，可得结论；
（2）BE=2AM+CE，同理得：△AEC≌△ADB，则CE=BD，再由等腰三角形三线合一及直角三角形斜边中线是斜边一半得：ED=2AM，则BE=2AM+CE；
（3）分两种情况：
根据∠BPD=90°，可以看作是：BP是以D为圆心以2为半径的圆的切线，
①如图3所示，作辅助线，构建等腰直角三角形和全等三角形，证明△ADP≌△ABE，则BE=PD=2，利用勾股定理求对角线BD和PB的长，再利用直角三角形斜边中线等于斜边一半得AF的长，代入面积公式可求得S_△ABP的值；
②如图4所示，同理可得结论．

解答 解：（1）CE=BD，理由是：
如图1，∵△ABC和△ADE都是等腰直角三角形，
∴AE=AD，AC=AB，
∵∠CAB=∠EAD=90°，
∴∠CAB-∠CAD=∠EAD-∠CAD，
即∠DAB=∠EAC，
∴△AEC≌△ADB，
∴CE=BD；
（2）BE=2AM+CE，理由是：
如图2，同理得：△AEC≌△ADB，
∴CE=BD，
∵△ADE是等腰直角三角形，AM⊥ED，
∴EM=DM，
∴ED=2AM，
∴BE=ED+BD=2AM+CE；
（3）∵PD=2，∠BPD=90°
∴BP是以D为圆心以2为半径的圆的切线，
①如图3所示，过A作AE⊥AP，交PB的延长线于E，连接BD，
∵∠DAB=∠DPB=90°，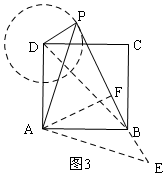
∴D、A、B、P四点共圆，
∴∠ADP+∠ABP=180°，
∵∠ABP+∠ABE=180°，
∴∠ADP=∠ABE，
∵四边形ABCD为正方形，
∴AD=AB，
∵∠DAP+∠PAB=90°，
∠PAB+∠BAE=90°，
∴∠DAP=∠BAE，
∴△ADP≌△ABE，
∴BE=PD=2，
∵AD=AB=5，
∴BD=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$，
在Rt△PDB中，PB=$\sqrt{（5\sqrt{2}）^{2}-{2}^{2}}$=$\sqrt{46}$，
∴PE=PB+BE=2+$\sqrt{46}$，
过A作AF⊥PB于F，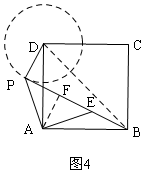
∴AF=$\frac{1}{2}$PE=$\frac{1}{2}$（2+$\sqrt{46}$）=1+$\frac{1}{2}$$\sqrt{46}$，
∴S_△ABP=$\frac{1}{2}$PB•AF=$\frac{1}{2}$×$\sqrt{46}$×$（1+\frac{1}{2}\sqrt{46}）$=$\frac{1}{2}$$\sqrt{46}$+$\frac{23}{2}$；
②如图4所示，过A作AE⊥AP，交PB于E，连接BD，
∵∠C=∠DPB=90°
∴D、C、B、P四点共圆，
∴∠CDP+∠CBP=180°，
∵∠ADC=90°
∴∠ADP+∠CBP=90°
∵∠ABP+∠CBP=90°，
∴∠ADP=∠ABE，
∵四边形ABCD为正方形，
∴AD=AB，
同理得：∠DAP=∠EAB，
∴△ADP≌△ABE，
∴BE=PD=2，
∵AD=AB=5，
∴BD=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$，
在Rt△PDB中，PB=$\sqrt{（5\sqrt{2}）^{2}-{2}^{2}}$=$\sqrt{46}$，
∴PE=PB-BE=$\sqrt{46}$-2，
过A作AF⊥PB于F，
∴AF=$\frac{1}{2}$PE=$\frac{1}{2}$（$\sqrt{46}$-2）=$\frac{1}{2}$$\sqrt{46}$-1，
∴S_△ABP=$\frac{1}{2}$PB•AF=$\frac{1}{2}$×$\sqrt{46}$×$（\frac{1}{2}\sqrt{46}-1）$=$\frac{23}{2}$-$\frac{1}{2}\sqrt{46}$；
综上所述，△ABP的面积为$\frac{1}{2}$$\sqrt{46}$+$\frac{23}{2}$或$\frac{23}{2}$-$\frac{1}{2}\sqrt{46}$．

点评 本题是四边形和三角形的综合题，考查了正方形的性质、四点共圆的性质和判定、三角形全等的性质和判定、等腰直角三角形的性质等知识，前两问构建全等三角形是关键，第三问构建辅助圆与切线是关键．