
| A. | 若添加条件AB=A′B′,则△ABC≌△A′B′C′ | |
| B. | 若添加条件∠C=∠C′,则△ABC≌△A′B′C′ | |
| C. | 若添加条件∠B=∠B′,则△ABC≌△A′B′C′ | |
| D. | 若添加条件BC=B′C′,则△ABC≌△A′B′C′ |
分析 根据各个选项中的说法可以三角形全等判定的条件可以判断选项中哪个的说法是正确的,哪个是错误的,本题得以解决.
解答 解:∵在△ABC与△A′B′C′中,已知∠A=∠A′,AC=A′C′,若AB=A′B′,则△ABC≌△A′B′C′(SAS),故选项A正确,
∵在△ABC与△A′B′C′中,已知∠A=∠A′,AC=A′C′,若∠C=∠C′,则△ABC≌△A′B′C′(ASA),故选项B正确,
∵在△ABC与△A′B′C′中,已知∠A=∠A′,AC=A′C′,若∠B=∠B′,则△ABC≌△A′B′C′(AAS),故选项C正确,
∵在△ABC与△A′B′C′中,已知∠A=∠A′,AC=A′C′,若BC=B′C′,则无法判定△ABC≌△A′B′C′,故选项D错误,
故选D.
点评 本题考查全等三角形的判定,解答此类问题的关键是明确题意,明确全等三角形判定的依据.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
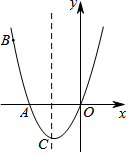 如图,已知抛物线C1经过A(-2,0),B(-3,3)及原点O,顶点为C.
如图,已知抛物线C1经过A(-2,0),B(-3,3)及原点O,顶点为C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 含有一个未知数的等式是一元一次方程 | |
| B. | 未知数的次数都是1次的方程是一元一次方程 | |
| C. | 含有一个未知数,并且未知数的次数都是一次的方程是一元一次方程 | |
| D. | 2t-7=1是一元一次方程 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+1 | B. | ±$\sqrt{a+1}$ | C. | a2+1 | D. | ±$\sqrt{{a}^{2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com