

分析 先利用勾股定理计算出AC=4,对于方案一:如图1,设正方形CGFE的边长为x,则BE=3-x,证明△BEF∽△BCA,利用相似比可计算出x=$\frac{12}{7}$;对于方案二:如图2,设正方形HGFE的边长为y,作CM⊥AB于M,交HG于N,利用面积法计算出CM=$\frac{12}{5}$,再证明△CHG∽△CBA,利用相似比可计算出y=$\frac{60}{37}$,然后比较x和y的大小即可判断哪种方案能裁出面积最大的正方形铁片.
解答 解:∠C=90°,AB=5cm,BC=3cm,则AC=$\sqrt{{5}^{2}-{3}^{2}}$=4,
方案一:如图1,设正方形CGFE的边长为x,则BE=3-x,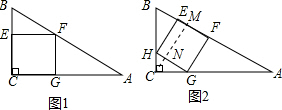 ∵EF∥AC,
∵EF∥AC,
∴△BEF∽△BCA,
∴$\frac{EF}{CA}$=$\frac{BE}{BC}$,即$\frac{x}{4}$=$\frac{3-x}{3}$,解得x=$\frac{12}{7}$;
方案二:如图2,设正方形HGFE的边长为y,作CM⊥AB于M,交HG于N,
∵$\frac{1}{2}$CM•AB=$\frac{1}{2}$•BC•AC,
∴CM=$\frac{3×4}{5}$=$\frac{12}{5}$,
∵HG∥AB,
∴△CHG∽△CBA,
∴$\frac{HG}{AB}$=$\frac{CN}{CM}$,即$\frac{y}{5}$=$\frac{\frac{12}{5}-y}{\frac{12}{5}}$,解得y=$\frac{60}{37}$,
∵x=$\frac{12}{7}$=$\frac{60}{35}$>$\frac{60}{37}$=y,
∴第一种方案能裁出面积最大的正方形铁片.
点评 本题考查了相似三角形的应用:常常构造“A”型或“X”型相似图,利用三角形相似的性质计算相应线段的长.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 30×106 | B. | 0.3×108 | C. | 3×108 | D. | 3×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
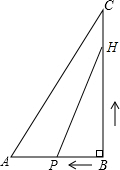 如图,在Rt△ABC中,∠B=90°,点P从点B开始沿BA边以1cm/s的速度向点A移动;同时,点H也从点B开始沿BC边以2cm/s的速度向点C移动.
如图,在Rt△ABC中,∠B=90°,点P从点B开始沿BA边以1cm/s的速度向点A移动;同时,点H也从点B开始沿BC边以2cm/s的速度向点C移动.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
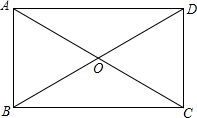 已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.求证:
已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?
某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com