
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其中点
,其中点![]() 的坐标为
的坐标为![]()

![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 若点
若点![]() 在抛物线上,且
在抛物线上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 设点
设点![]() 是线段
是线段![]() 上的动点,作
上的动点,作![]() 轴交抛物线于点
轴交抛物线于点![]() ,求线段
,求线段![]() 长度的最大值.
长度的最大值.
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 于
于![]() ,
,![]() 于
于![]() ,要计算
,要计算![]() ,
,![]() 两地的距离,甲、乙、丙、丁四组同学分别测量了部分线段的长度和角的度数,得到以下四组数据:甲:
两地的距离,甲、乙、丙、丁四组同学分别测量了部分线段的长度和角的度数,得到以下四组数据:甲:![]() ,
,![]() ;乙:
;乙:![]() ,
,![]() ,
,![]() ;丙:
;丙:![]() 和
和![]() ;丁:
;丁:![]() ,
,![]() ,
,![]() .其中能求得
.其中能求得![]() ,
,![]() 两地距离的有( )
两地距离的有( )

A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AD为△ABC的中线,延长AD至E,使DE=AD.
(1)试证明:△ACD≌△EBD;
(2)用上述方法解答下列问题:如图2,AD为△ABC的中线,BMI交AD于C,交AC于M,若AM=GM,求证:BG=AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于抛物线![]() .
.

对于抛物线![]() .
.
![]() 它与
它与![]() 轴交点的坐标为________,与
轴交点的坐标为________,与![]() 轴交点的坐标为________,顶点坐标为________.
轴交点的坐标为________,顶点坐标为________.
![]() 在所给的平面直角坐标系中画出此时抛物线;
在所给的平面直角坐标系中画出此时抛物线;
![]() 结合图象回答问题:当
结合图象回答问题:当![]() 时,
时,![]() 的取值范围是________.
的取值范围是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有【 】
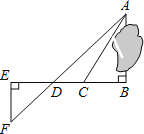
A.1组 B.2组 C.3组 D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知∠MAN=135°,正方形ABCD绕点A旋转.
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是 ;
②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 可看成是分别以
可看成是分别以![]() 、
、![]() 、
、![]() 、
、![]() 为位似中心将正方形
为位似中心将正方形![]() 放大一倍得到的图形(正方形
放大一倍得到的图形(正方形![]() 的边长放大到原来的
的边长放大到原来的![]() 倍),由正方形
倍),由正方形![]() 到正方形
到正方形![]() ,我们称之作了一次变换,再将正方形
,我们称之作了一次变换,再将正方形![]() 作一次变换就得到正方形
作一次变换就得到正方形![]() ,…,依此下去,作了
,…,依此下去,作了![]() 次变换后得到正方形
次变换后得到正方形![]() ,若正方形
,若正方形![]() 的面积是
的面积是![]() ,那么正方形
,那么正方形![]() 的面积是多少( )
的面积是多少( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com