
【题目】如图1,AD为△ABC的中线,延长AD至E,使DE=AD.
(1)试证明:△ACD≌△EBD;
(2)用上述方法解答下列问题:如图2,AD为△ABC的中线,BMI交AD于C,交AC于M,若AM=GM,求证:BG=AC.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据中线的定义,即可得到BD=CD,再根据SAS即可判定△ACD≌△EBD.
(2)延长AD到F,使AD=DF,连接BF,根据SAS证△ADC≌△FDB,推出BF=AC,∠CAD=∠F,根据AM=GM,推出∠CAD=∠AGM=∠BGF,求出∠BGF=∠F,根据等腰三角形的性质求出即可.
(1)证明:∵AD是△ABC的中线,
∴BD=CD,
在△ACD和△EBD中,
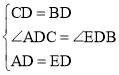 ,
,
∴△ACD≌△EBD(SAS).
(2)证明:延长AD到F,使AD=DF,连接BF,
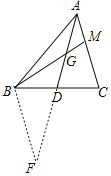
∵AD是△ABC中线,
∴BD=DC,
∵在△ADC和△FDB中
 ,
,
∴△ADC≌△FDB(SAS),
∴BF=AC,∠CAD=∠F,
∵AM=GM,
∴∠CAD=∠AGM,
∵∠AGM=∠BGF,
∴∠BGF=∠CAD=∠F,
∴BG=BF=AC,
即BG=AC.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:
【题目】已知,![]() 为等边三角形,点
为等边三角形,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合).以
重合).以![]() 为边作菱形
为边作菱形![]() ,使
,使![]() ,连接
,连接![]() .
.
![]() 如图
如图![]() ,当点
,当点![]() 在边
在边![]() 上时,
上时,
①求证:![]() ;②请直接判断结论
;②请直接判断结论![]() 是否成立;
是否成立;
![]() 如图
如图![]() ,当点
,当点![]() 在边
在边![]() 的延长线上时,其他条件不变,结论
的延长线上时,其他条件不变,结论![]() 是否成立?请写出
是否成立?请写出![]() 、
、![]() 、
、![]() 之间存在的数量关系,并写出证明过程;
之间存在的数量关系,并写出证明过程;
![]() 如图
如图![]() ,当点
,当点![]() 在边
在边![]() 的延长线上时,且点
的延长线上时,且点![]() 、
、![]() 分别在直线
分别在直线![]() 的异侧,其他条件不变,请补全图形,并直接写出
的异侧,其他条件不变,请补全图形,并直接写出![]() 、
、![]() 、
、![]() 之间存在的等量关系.
之间存在的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AB=12cm,AD=5cm,E是DC上一点(点E不与D、C重合)连接AE,以AE所在的直线为折痕,折叠纸片,点D的对应点为D′,点F为线段BC上一点,连接EF,以EF所在的直线为折痕折叠纸片,使点C的对应点C′落在直线ED′上,若CF=4时,DE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线BC:![]() ,直线BD与x轴交于点A,点B(2,3),点D(0,
,直线BD与x轴交于点A,点B(2,3),点D(0,![]() ).
).
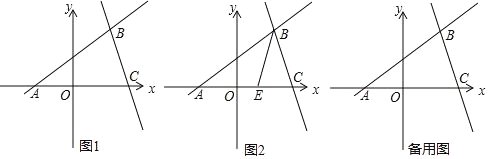
(1)求直线BD的函数解析式;
(2)在y轴上找一点P,使得△ABC与△ACP的面积相等,求出点P的坐标;
(3)如图2,E为线段AC上一点,连结BE,一动点F从点B出发,沿线段BE以每秒1个单位运动到点E再沿线段EA以每秒![]() 个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AB=12cm,AD=5cm,E是DC上一点(点E不与D、C重合)连接AE,以AE所在的直线为折痕,折叠纸片,点D的对应点为D′,点F为线段BC上一点,连接EF,以EF所在的直线为折痕折叠纸片,使点C的对应点C′落在直线ED′上,若CF=4时,DE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)为加强与家长的沟通,某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传,该校的印刷任务原来由甲复印店承接,其收费y(元)与印刷页数x(页)的函数关系如图所示.

(1)从图象中可看出:印刷超过500页部分每页收费 元;
(2)现在乙印刷厂表示:每页0.15元收费.另收200元的制版费,乙印刷厂收费y(元)与印刷页数x(页)的函数关系为 ;
(3)在给出的坐标系内画出(2)中的函数图象,并结合函数图象回答印刷页数在3000页左右应选择哪个印刷店?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
,![]() 是
是![]() 的
的![]() 边上的中点,过点
边上的中点,过点![]() 的一条直线交
的一条直线交![]() 于
于![]() ,交
,交![]() 的延长线于
的延长线于![]() ,
,![]() 交
交![]() 于
于![]() ,我们可以证明
,我们可以证明![]() 成立(不要求考生证明).
成立(不要求考生证明).
![]() 如图
如图![]() ,若将图
,若将图![]() 中的过点
中的过点![]() 的一条直线交
的一条直线交![]() 于
于![]() ,改为交
,改为交![]() 的延长线于
的延长线于![]() ,交
,交![]() 的延长线于
的延长线于![]() ,改为交
,改为交![]() 于
于![]() ,其它条件不变,则
,其它条件不变,则![]() 还成立吗?如果成立,请给出证明;如果不成立,请说出理由;
还成立吗?如果成立,请给出证明;如果不成立,请说出理由;
![]() 根据图
根据图![]() ,请你找出
,请你找出![]() 、
、![]() 、
、![]() 、
、![]() 四条线段之间的关系,并给出证明;
四条线段之间的关系,并给出证明;
![]() 如图
如图![]() ,若将图
,若将图![]() 中的过点
中的过点![]() 的一条直线交
的一条直线交![]() 于
于![]() ,改为交
,改为交![]() 的反向延长线于
的反向延长线于![]() ,交
,交![]() 的延长线于
的延长线于![]() ,改为交
,改为交![]() 于
于![]() ,其它条件不变,则
,其它条件不变,则![]() 得到的结论是否成立?
得到的结论是否成立?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其中点
,其中点![]() 的坐标为
的坐标为![]()

![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 若点
若点![]() 在抛物线上,且
在抛物线上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 设点
设点![]() 是线段
是线段![]() 上的动点,作
上的动点,作![]() 轴交抛物线于点
轴交抛物线于点![]() ,求线段
,求线段![]() 长度的最大值.
长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般地,“任意三角形都是自相似图形”,只要顺次连接三角形各边中点,则可将原三角形分割为四个都与它自己相似的小三角形.我们把![]() (图乙)第一次顺次连接各边中点所进行的分割,称为
(图乙)第一次顺次连接各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() );把
);把![]() 阶分割得出的
阶分割得出的![]() 个三角形再分别顺次连接它的各边中点所进行的分割,称为
个三角形再分别顺次连接它的各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() )…,依此规则操作下去.
)…,依此规则操作下去.![]() 阶分割后得到的每一个小三角形都是全等三角形(
阶分割后得到的每一个小三角形都是全等三角形(![]() 为正整数),设此时小三角形的面积为
为正整数),设此时小三角形的面积为![]() .请写出一个反映
.请写出一个反映![]() ,
,![]() ,
,![]() 之间关系的等式________.
之间关系的等式________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com