
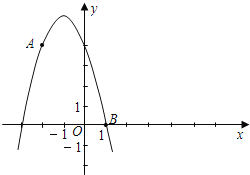
【题目】如图已知点A (﹣2,4)和点B (1,0)都在抛物线y=mx2+2mx+n上.
(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′的交点为点C,试在x轴上找点D,使得以点B′、C、D为顶点的三角形与△ABC相似.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)已知了抛物线图象上A、B两点的坐标,将它们代入抛物线的解析式中,即可求得m、n的值.
(2)根据A、B的坐标,易求得AB的长;根据平移的性质知:四边形AA′B′B一定为平行四边形,若四边形AA′B′B为菱形,那么必须满足AB=BB′,由此可确定平移的距离,根据“左加右减”的平移规律即可求得平移后的抛物线解析式.
(3)易求得直线AB′的解析式,联立平移后的抛物线对称轴,可得到C点的坐标,进而可求出AB、BC、AC、B′C的长;在(2)题中已经证得AB=BB′,那么∠BAC=∠BB′C,即A、B′对应,若以点B′、C、D为顶点的三角形与△ABC相似,可分两种情况考虑:①∠B′CD=∠ABC,此时△B′CD∽△ABC,②∠B′DC=∠ABC,此时△B′DC∽△ABC;
根据上述两种不同的相似三角形所得不同的比例线段,即可求得不同的BD长,进而可求得D点的坐标.
解:(1)由于抛物线经过A (﹣2,4)和点B (1,0),则有:
![]() ,解得
,解得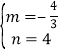 ;
;
故m=﹣![]() ,n=4.
,n=4.
(2)由(1)得:y=﹣![]() x2﹣
x2﹣![]() x+4=﹣
x+4=﹣![]() (x+1)2+
(x+1)2+![]() ;
;
由A (﹣2,4)、B (1,0),可得AB=![]() =5;
=5;
若四边形A A′B′B为菱形,则AB=BB′=5,即B′(6,0);
故抛物线需向右平移5个单位,即:
y=﹣![]() (x+1﹣5)2+
(x+1﹣5)2+![]() =﹣
=﹣![]() (x﹣4)2+
(x﹣4)2+![]() .
.
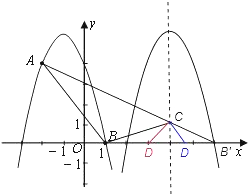
(3)由(2)得:平移后抛物线的对称轴为:x=4;
∵A(﹣2,4),B′(6,0),
∴直线AB′:y=﹣![]() x+3;
x+3;
当x=4时,y=1,故C(4,1);
所以:AC=3![]() ,B′C=
,B′C=![]() ,BC=
,BC=![]() ;
;
由(2)知:AB=BB′=5,即∠BAC=∠BB′C;
若以点B′、C、D为顶点的三角形与△ABC相似,则:
①∠B′CD=∠ABC,则△B′CD∽△ABC,可得:
![]() =
=![]() ,即
,即![]() =
=![]() ,B′D=3,
,B′D=3,
此时D(3,0);
②∠B′DC=∠ABC,则△B′DC∽△ABC,可得:
![]() =
=![]() ,即
,即![]() =
=![]() ,B′D=
,B′D=![]() ,
,
此时D(![]() ,0);
,0);
综上所述,存在符合条件的D点,且坐标为:D(3,0)或(![]() ,0).
,0).
“点睛”此题考查了二次函数解析式的确定、函数图象的平移、菱形的判定和性质、相似三角形的判定和性质等知识;(3)题中,在相似三角形的对应角和对应边不确定的情况下,一定要分类讨论,以免漏解.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )

A. 6→3 B. 7→16 C. 7→8 D. 6→15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ≈1.7,结果精确到个位).
≈1.7,结果精确到个位).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B:党史手抄报比赛,C:党史知识竞赛,D:红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:
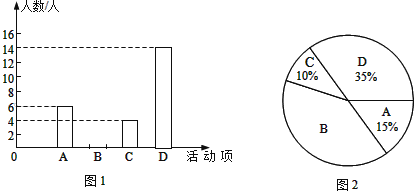
(1)本次共调查了 名学生;
(2)将图1的统计图补充完整;
(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
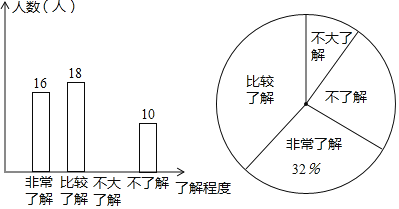
【题目】某校为了解学生对“第二十届中国哈尔滨冰雪大世界”主题景观的了解情况,在全体学生中随机抽取了部分学生进行调查,并把调查结果绘制成如图的不完整的两幅统计图:
(1)本次调查共抽取了多少名学生;
(2)通过计算补全条形图;
(3)若该学校共有![]() 名学生,请你估计该学校选择“比较了解”项目的学生有多少名?
名学生,请你估计该学校选择“比较了解”项目的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
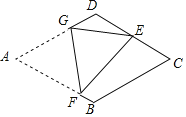
【题目】如图,在菱形纸片ABCD中,AB=4,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则sin∠EFG的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
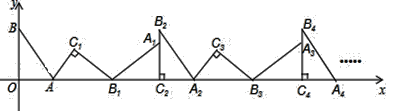
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(3,0),B(0,4),则点B2018的坐标为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com