Question

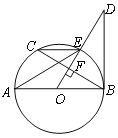
【题目】如图，在△OAB中，OA=OB，以点O为圆心的⊙O经过AB的中点C，直线AO与⊙O相交于点E、D，OB交⊙O于点F，P是 的中点，连接CE、CF、BP．

（1）求证：AB是⊙O的切线．

（2）若OA=4，则

①当长为_____时，四边形OECF是菱形；

②当 长为_____时，四边形OCBP是正方形．

Answer 1

【答案】（1）证明见解析；（2）①；②．

【解析】

(1)证明垂直就可以证明是切线.(2)利用四边形OECF是菱形的性质反推可得到DP长.利用正方形OECF的性质反推可得到DP长.

解：（1）∵在△ABO中，OA=OB，C是AB的中点，

∴OC⊥AB．

∵OC为⊙O的半径，

∴AB是⊙O的切线．

（2）①∵OECF为菱形，

∴OE=EC，∠EOC=∠COF．

∴OE=EC=OC．

∴∠EOC=∠COF=60°．

∴∠DOF=60°．

又∵P为弧DF的中点，

∴∠DOP=30°．

∵∠AOC=60°，∠OCA=90°，

∴OC=OA=2．

∴弧DP的长=.

②∵四边形OCBP为正方形，

∴∠COB=∠POB=45°．

∴OC=OB=2．

∵P为弧DF的中点，

∴∠DOP=45°．

∴弧DP的长=．

故答案为：①；②．