
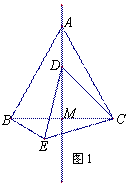
如图8所示,在等边△ABC中,线段AM为BC边上的中线. 动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)填空:∠CAM= 度;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
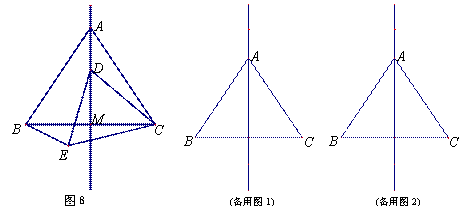 (3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
(3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
解: (1)30;………………………………………………………..1分
(2)∵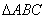 与
与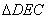 都是等边三角形
都是等边三角形
∴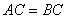 ,
,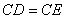 ,
,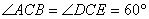 ……………….2分
……………….2分
∴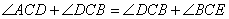
 ∴
∴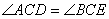
∴ ≌
≌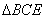
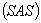 …………………………………………...3分
…………………………………………...3分
(3) 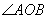 是定值,
是定值,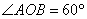 ,理由如下:
,理由如下:
①当点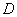 在线段
在线段 上时,如图1,由(2)可知
上时,如图1,由(2)可知 ≌
≌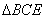 ,
,
则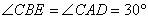 ,又
,又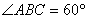
∴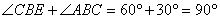 ………………………..............4分
………………………..............4分
 ∵
∵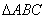 是等边三角形,线段
是等边三角形,线段 为
为 边上的中线
边上的中线
∴ 平分
平分 ,即
,即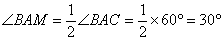
∴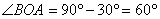 ………………………………5分
………………………………5分
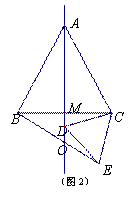
②当点 在线段
在线段 的延长线上时,如图2,
的延长线上时,如图2,
∵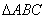 与
与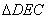 都是等边三角形
都是等边三角形
∴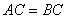 ,
,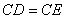 ,
,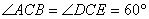
∴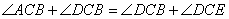 ,∴
,∴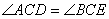
∴ ≌
≌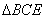
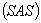 ………………………………...6分
………………………………...6分
∴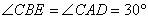 ,同理可得:
,同理可得: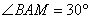 ,∴
,∴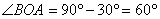 …………………………………….7分
…………………………………….7分
 ③当点
③当点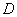 在线段
在线段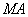 的延长线上时,
的延长线上时,
∵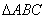 与
与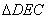 都是等边三角形
都是等边三角形
∴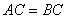 ,
,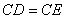 ,
,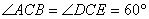
∴
∴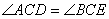
∴ ≌
≌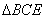
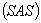 ……………………………….8分
……………………………….8分
∴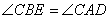
同理可得: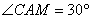
∴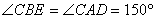
∴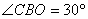 ,
,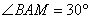 ,∴
,∴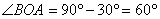 ……………9分
……………9分


科目:初中数学 来源: 题型:
用反证法证明命题“钝角三角形中必有一个内角小于 45°”时,首先应该假设这个三角形中( )
A.有一个内角小于 45° B.每一个内角都小于 45°
C.有一个内角大于等于 45° D.每一个内角都大于等于 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
定义运算 ◆
◆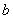 =
=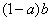 ,下面给出了关于这种运算的四个结论:
,下面给出了关于这种运算的四个结论:
①2◆(-2)=3 ② ◆
◆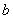 =
=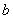 ◆
◆
③若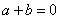 ,则(
,则( ◆
◆ )+(
)+(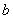 ◆★
◆★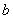 )=2
)=2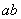
④若 ◆
◆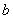 =0,则
=0,则 =1或
=1或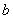 =0.
=0.
其中正确结论的序号是 (填上你认为正确的所有结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
为了解今年初二学生的数学学习情况,某校在第一轮模拟测试后,对初二全体同学的数学成绩作了统计分析,绘制如下图表:
请结合图表所给出的信息解答下列问题:
(1)该校初二
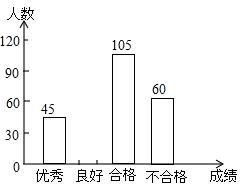
学生共有多少人?
(2)求表中 ,b,c的值,并补全条形统计图;
,b,c的值,并补全条形统计图;
查看答案和解析>>
科目:初中数学 来源: 题型:
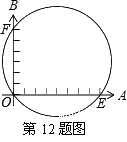
如图,小明同学设计了一个测量圆直径的工具,标有刻度的尺OA、OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为
 A.10个单位
A.10个单位
B.12个单位
C.1个单位
D.15个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
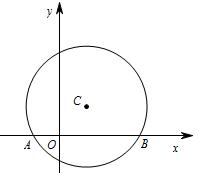
如图,在平面直角坐标系中,以点C(1,1) 为圆心,2 为半径作圆,交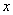 轴于A,B 两点,点 P在 ⊙C上.
轴于A,B 两点,点 P在 ⊙C上.
(1) 求出A,B 两点的坐标;
(2) 试确定经过 A、 B两点且以点 P为顶点的抛物线解析式;
(3) 在该抛物线上是否存在一点D,使线段 OP与CD 互相平分?若存在,求出点 D 的坐标;若不存在,请说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com