
【题目】如图,⊙![]() 和⊙
和⊙![]() 相交于A、B两点,
相交于A、B两点,![]() 与AB交于点C,
与AB交于点C,![]() 的延长线交⊙
的延长线交⊙![]() 于点D,点E为AD的中点,AE=AC,联结
于点D,点E为AD的中点,AE=AC,联结![]() .
.
(1)求证:![]() ;
;
(2)如果![]() ,
,![]() ,求⊙
,求⊙![]() 的半径长.
的半径长.
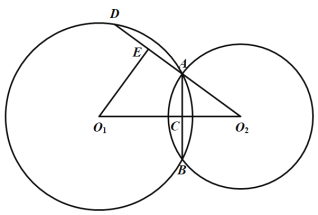
【答案】(1)证明见解析;(2)5.
【解析】
(1)根据条件得到AC,AB的关系,再利用AC=AB即可解答.
(2)利用三角形相似即可解答.
⑴ ⊙O1和⊙O2相交于A、B两点,
∴O1O2是AB的垂直平分线
∴AB=2AC,
∵E为AD的中点
∴AD=2AE,O1E⊥AD,
∵AE=AC,
∴AB=AD,
∴O1E=O1C.
⑵ ∵O1E⊥AD,
∴∠O1EO2=90°,
在RT△O1EO2中,∠O1EO2=90°,O1O2=10,O1E=6,
∵O1E2+O2E2=O1O22,
O2E2=102-62=64,
∴O2E=8,
∵∠O1EO2=∠O2CA=90°,
∠O2=∠O2,
∴△O2EO1∽△O2CA,
∴![]() ,
,
∵O1O2=10,
AC=AE=O2E-O2A=8-O2A,O1E=6,
∴![]() ,
,
∴![]() A=5.
A=5.
即⊙![]() 的半径长为5.
的半径长为5.
故答案为5.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
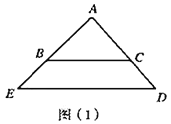
【题目】(1)问题发现:
如图(1),![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,点
,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,请直接写出线段
上,请直接写出线段![]() 与
与![]() 的数量关系:______;(直接填写结果)
的数量关系:______;(直接填写结果)
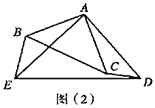
(2)操作探究:
如图(2),将图中的![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() (
(![]() ),I小题中线段
),I小题中线段![]() 与线段
与线段![]() 的数量关系是否成立?如果不成立,说明理由,如果成立,请你结合图(2)给出的情形进行证明;
的数量关系是否成立?如果不成立,说明理由,如果成立,请你结合图(2)给出的情形进行证明;
(3)解决问题:
将图(1)中的![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,若
,若![]() ,在备用图中画出旋转图形,并判断以
,在备用图中画出旋转图形,并判断以![]() 、
、![]() 、
、![]() 、
、![]() 四个点为顶点的四边形的形状.(不写证明过程)
四个点为顶点的四边形的形状.(不写证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
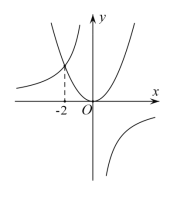
【题目】过反比例函数 y= ![]() (k < 0)的图象上一点 A 作 x 轴的垂线交 x 轴于点 B ,O 为坐标原点, 且△ABO 的面积 S△ABO = 4 .
(k < 0)的图象上一点 A 作 x 轴的垂线交 x 轴于点 B ,O 为坐标原点, 且△ABO 的面积 S△ABO = 4 .
(1)求 k 的值;
(2)若二次函数 y = ax2 与反比例函数 y= ![]() (k < 0)的图象交于点C(-2,m) ,请结合函数的图象写出满足 ax2<
(k < 0)的图象交于点C(-2,m) ,请结合函数的图象写出满足 ax2< ![]() 的x的取值范围.
的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泉州市旅游资源丰富,①清源山、②开元寺、③崇武古城三个景区是人们节假日玩的热点景区,张老师对八(1)班学生“五·一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别:A、游三个景区;B,游两个景区;C,游一个景区:D,不到这三个景区游玩现根据调查结果绘制了不完整的条形统计图和廟形统计图,请结合图中信息解答下列问题:
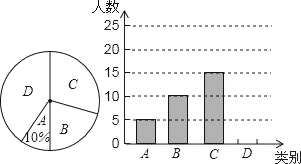
(1)八(1)班共有学生 人在扇形统计图中,表示“B类别的扇形的圆心角的度数为 ;
(2)请将条形统计图补充完整;
(3)若小华、小刚两名同学,各自从三个最区中随机选一个作为5月1日游玩的景区,请用树状图或列表法求他们选中同个景区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AD∥BC,AB=DC,E是对角线AC上一点,且AC·CE=AD·BC.
(1)求证:∠DCA=∠EBC;
(2)延长BE交AD于F,求证:AB2=AF·AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2+4x﹣9=0时,原方程可变形为( )
A. (x+2)2=1 B. (x+2)2=7 C. (x+2)2=13 D. (x+2)2=19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=![]() 的图象经过点A,反比例函数y2=﹣
的图象经过点A,反比例函数y2=﹣![]() 的图象经过点B,则m的值是( )
的图象经过点B,则m的值是( )

A.m=3B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com