
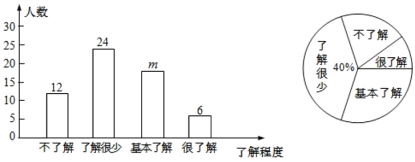
【题目】2019年12月以来,湖北省武汉市部分医院陆续发现不明原因肺炎病例,现已证实该肺炎为一种新型冠状病毒感染的肺炎,其传染性较强.为了有效地避免交叉感染,需要采取以下防护措施:①戴口罩;②勤洗手;③少出门;④重隔离;⑤捂口鼻;⑥谨慎吃.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制成如下两幅统计图.
请你根据上面的信息,解答下列问题
(1)本次共调查了_______名员工,条形统计图中![]() ________;
________;
(2)若该公司共有员工1000名,请你估计不了解防护措施的人数;
(3)在调查中,发现有4名员工对防护措施很了解,其中有3名男员工、1名女员工.若准备从他们中随机抽取2名,让其在公司群内普及防护措施,求恰好抽中一男一女的概率.
【答案】(1)60 ,18;(2)估计不了解防护措施的人数为200名;(3)恰好抽中一男一女的概率为![]() .
.
【解析】
(1)用“了解很少”的人数除以它所占的比例即可得到调查的总人数,再用总人数减去“不了解”的人数、“了解很少”的人数及“很了解”的人数即可得到m;
(2)用1000乘以样本中“不了解”的人数所占的比例即可;
(3)列表展示出所有12种等可能的结果数,再找出恰好抽中一男一女的结果数,然后根据概率公式即可求解.
(1)由统计图可知,“了解很少”的员工有24名,其所占的百分比为40%,
故本次调查的员工人数为![]() (名),
(名),
∴![]() ,
,
故答案为:60 ,18;
(2)![]() (名).
(名).
答:估计不了解防护措施的人数为200名.
(3)根据题意,列表如下:
第1名 | 第2名 | |||
|
|
| 女 | |
|
|
|
| |
|
|
|
| |
|
|
|
| |
女 |
|
|
| |
由上表可知,共有12种结果,每种结果出现的可能性都相等,其中恰好抽中一男一女的结果有6种,
故所求概率为![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】某水果经销商上月份销售一种新上市的水果,平均售价为10元/千克,月销售量为1000千克.经市场调查,若将该种水果价格调低至x元/千克,则本月份销售量y(千克)与x(元/千克)之间符合一次函数关系,并且得到了表中的数据:
价格x(元/千克) | 7 | 5 |
价格y(千克) | 2000 | 4000 |
(1)求y与x之间的函数解析式;
(2)已知该种水果上月份的成本价为5元/千克,本月份的成本价为4元/千克,要使本月份销售该种水果所获利润比上月份增加20%,同时又要让顾客得到实惠,那么该种水果价格每千克应调低至多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在等腰![]() 中,如图①,在等腰
中,如图①,在等腰![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .点
.点![]() 为线段
为线段![]() 上一点(不与端点
上一点(不与端点![]() 、
、![]() 重合),
重合),![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
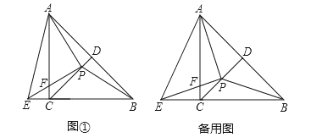
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)探究线段![]() 、
、![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
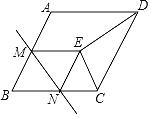
【题目】如图,在菱形ABCD中,∠B=60°,AB=2,M为边AB的中点,N为边BC上一动点(不与点B重合),将△BMN沿直线MN折叠,使点B落在点E处,连接DE、CE,当△CDE为等腰三角形时,BN的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)P是抛物线上的第一象限内的动点,过点P作PMx轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.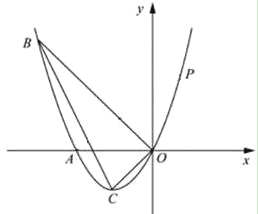
查看答案和解析>>
科目:初中数学 来源: 题型:
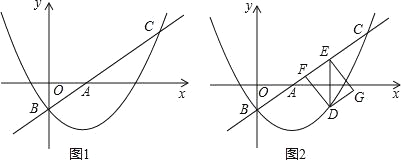
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】"桃花流水窅然去,别有天地非人间."桃花园景点2017年三月共接待游客![]() 万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加
万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加![]() ,则可列方程为( )
,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
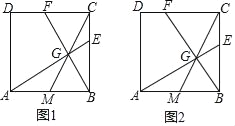
【题目】已知正方形ABCD,点M为边AB的中点.
(1)如图1,点G为线段CM上的一点,且∠AGB=90°,延长AG、BG分别与边BC、CD交于点E、F.
①求证:BE=CF;
②求证:BE2=BCCE.
(2)如图2,在边BC上取一点E,满足BE2=BCCE,连接AE交CM于点G,连接BG并延长交CD于点F,求tan∠CBF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于任意三点A,B,C,给出如下定义:若矩形的任何一条边均与某条坐标轴平行或重合,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的外延矩形,点A,B,C的所有外延矩形中,面积最小的矩形称为点A,B,C的最佳外延矩形.例如,图①中的矩形A1B1C1D1,A2B2C2D2,A3B3CD3,都是点A,B,C的外延矩形,矩形A3B3CD3是点A,B,C的最佳外延矩形.
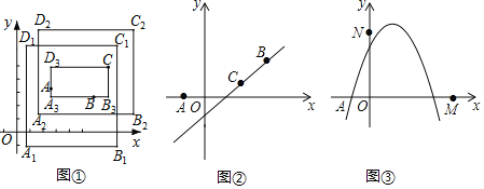
(1)如图②,已知A(﹣1,0),B(3,2),点C在直线y=x﹣1上,设点C的横坐标为t.
①若t=![]() ,则点A,B,C的最佳外延矩形的面积为多少?
,则点A,B,C的最佳外延矩形的面积为多少?
②若点A,B,C的最佳外延矩形的面积为9,求t的值.
(2)如图③,已知点M(4,0),N(0,![]() ),P(x,y)是抛物线y=﹣x2+2x+3上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标x的取值范围;
),P(x,y)是抛物线y=﹣x2+2x+3上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标x的取值范围;
(3)已知D(1,0).若Q是抛物线y=﹣x2﹣2mx﹣m2+2m+1的图象在﹣2≤x≤1之间的最高点,点E的坐标为(0,4m),设点D,E,Q的最佳外延矩形的面积为S,当4≤S≤6时,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com