
分析 (1)平行于墙的篱笆的长为x,那么垂直于墙的篱笆长为$\frac{1}{2}$(48-x),然后利用矩形的面积公式列出函数关系式,然后根据二次函数的性质解答即可;
(2)由(1)可知当a>24时,最大面积为288,当a<24时,最大面积=-$\frac{1}{2}(a-24)^{2}+288$;
(3)设靠墙的一面的矩形长为x米,则BC=48-2x,然后根据矩形的面积公式列出函数关系式即可;
(4)根据y的取值范围,列出不等式组,然后求得不等式组的解集即可.
解答 解:(1)设矩形花圃的面积为y,BC长为xm,则AB长为$\frac{1}{2}$(48-x)m.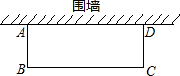
依题意,得y=$\frac{1}{2}$x(48-x)=-$\frac{1}{2}$(x-24)2+288.
∴抛物线的对称轴方程为x=24.
∵a=-$\frac{1}{2}$<0,
∴当x<24时,y随x的增大而增大.
当残墙为12米时,所围矩形花圃的最大面积=$-\frac{1}{2}(12-24)^{2}+288$=216;
当残墙为20米时,所围矩形花圃的最大面积=-$\frac{1}{2}(20-24)^{2}$+288=280;
当残墙为28米时,x=24,所围矩形花圃的最大面积=288;
∴当x=12m时,S最大=144m2,
故答案为:216;280;288;
(2)由(1)可知,当a≥24时,S=288m2;
当0<a<24时,S=$-\frac{1}{2}(a-24)^{2}+288$;
(3)设AB=x,则BC=48-2x.
由矩形的面积公式得:y=(48-2x)x=-2(x-12)2+288;
(4)∵a=14,
∴48-2x≤14.
∴x≥17.
∵84≤y≤238,
∴$\left\{\begin{array}{l}{-2(x-12)^{2}+288≥84①}\\{-2(x-12)^{2}≤238②}\end{array}\right.$
解得:19≤x≤22.
∴x的取值范围是:19≤x≤22.
点评 本题主要考查的是二次函数的应用,根据题意列出函数关系式是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
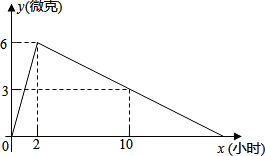 某医药研究所研发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时血液中含药量最高,达每毫升6微克,接着逐步衰减,服药后10小时血液中含药量为3微克,含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后.
某医药研究所研发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时血液中含药量最高,达每毫升6微克,接着逐步衰减,服药后10小时血液中含药量为3微克,含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+3)(x+5) | B. | (x-3)(x-5) | C. | (x-3)(x+5) | D. | (x+3)(x-5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com