
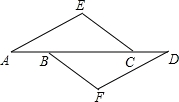
如图,在△AEC和△DFB中,∠E=∠F,点A、B、C、D在同一直线上,有如下三个关系式:①AE∥DF,②AB=CD,③CE=BF.
(1)请用其中两个关系式作为条件,另一个作为结论,写出你认为正确的所有命题(用序号写出命题书写形式:“如果⊗、⊗,那么⊗”)
(2)选择(1)中你写出的一个命题,说明它正确的理由.
【考点】全等三角形的判定与性质.
【专题】压轴题;开放型.
【分析】(1)如果①②作为条件,③作为结论,得到的命题为真命题;如果①③作为条件,②作为结论,得到的命题为真命题,写成题中要求的形式即可;
(2)若选择(1)中的如果①②,那么③,由AE与DF平行,利用两直线平行内错角相等得到一对角相等,再由AB=DC,等式左右两边都加上BC,得到AC=DB,又∠E=∠F,利用AAS即可得到三角形ACE与三角形DBF全等,根据全等三角形的对应边相等得到CE=BF,得证;若选择如果①③,那么②,由AE与FD平行,利用两直线平行内错角相等得到一对角相等,再由∠E=∠F,CE=BF,利用AAS可得出三角形ACE与三角形DBF全等,根据全等三角形的对应边相等可得出AC=BD,等式左右两边都减去BC,得到AB=CD,得证.
【解答】解:(1)如果①②,那么③;如果①③,那么②;
(2)若选择如果①②,那么③,
证明:∵AE∥DF,
∴∠A=∠D,
∵AB=CD,
∴AB+BC=BC+CD,即AC=DB,
在△ACE和△DBF中,
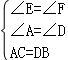 ,
,
∴△ACE≌△DBF(AAS),
 ∴CE=BF;
∴CE=BF;
若选择如果①③,那么②,
证明:∵AE∥DF,
∴∠A=∠D,
在△ACE和△DBF中,
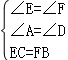 ,
,
∴△ACE≌△DBF(AAS),
∴AC=DB,
∴AC﹣BC=DB﹣BC,即AB=CD.
【点评】此题考查了全等三角形的判定与性质,平行线的性质,利用了转化的数学思想,熟练掌握全等三 角形的判定与性质是解本题的关键.
角形的判定与性质是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,在Rt直角△ABC中,∠B=45°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
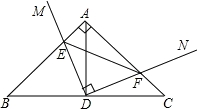
A.①②④ B.②③④ C.①②③ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
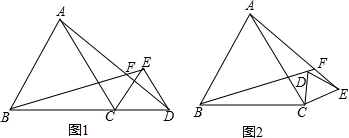
(1)如图1,C为线段BD上的一个动点(不与点B、D重合),在BD同侧分别作等边△ABC和等边△CDE,AD与BE相交于点F,求证:△ACD≌△BCE.
(2)将△CDE绕C点旋转至如图2,在旋转过程中,∠AFB的大小是否发生改变?若不改变,请求出∠AFB的度数;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )

A.48° B.36° C.30° D.24°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com