
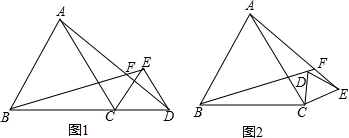
(1)如图1,C为线段BD上的一个动点(不与点B、D重合),在BD同侧分别作等边△ABC和等边△CDE,AD与BE相交于点F,求证:△ACD≌△BCE.
(2)将△CDE绕C点旋转至如图2,在旋转过程中,∠AFB的大小是否发生改变?若不改变,请求出∠AFB的度数;若改变,请说明理由.
【考点】全等三角形的判定与性质;等边三角形的性质.
【分析】(1)根据等边三角形的性质得到AC=BC,CE=CD,∠ACB=∠DCE=60°,求得∠BCE=∠ACD,即可得到结论;
(2)根据等边三角形的性质得到AC=BC,CE=CD,∠ACB=∠DCE=60°,推出△ACE≌△BCD,由全等三角形的性质得到∠CAF=∠CBF,由对顶角相等得到∠AOF=∠BOC,即可得到结论.
【解答】(1)证明:在等边△ABC和等边△CDE中,
∵AC=BC,CE=CD,∠ACB=∠DCE=60°,
∴∠BCE=∠ACD,
在△BCE与△ACD中,
 ,
,
∴△ACD≌△BCE;
(2)不改变,
理由:在等边△ABC和等边△CDE中,
∵AC=BC,CE=CD,∠ACB=∠DCE=60°,
∴∠BCE=∠ACD,
在△BCD与△ACE中,
 ,
,
∴△ACE≌△BCD,
∴∠CAF=∠CBF,
∵∠AOF=∠BOC,
∴∠AFB=∠ACB=60°,
∴∠AFB的大小不发生改变.

【点评】本题考查了全等三角形的判定和性质,等边三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
随着电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.000 000 74mm2,这个数用科学记数法表示为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
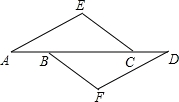
如图,在△AEC和△DFB中,∠E=∠F,点A、B、C、D在同一直线上,有如下三个关系式:①AE∥DF,②AB=CD,③CE=BF.
(1)请用其中两个关系式作为条件,另一个作为结论,写出你认为正确的所有命题(用序号写出命题书写形式:“如果⊗、⊗,那么⊗”)
(2)选择(1)中你写出的一个命题,说明它正确的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知(﹣2,y1),(﹣1.5,y2),(1,y3)是直线y=2x+b(b为常数)上的三个点,则y1,y2,y3的大小关系是__________.(用“>”表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com