
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )

A.48° B.36° C.30° D.24°
A【考点】线段垂直平分线的性质.
【分析】根据角平分线的性质可得∠DBC=∠ABD=24°,然后再计算出∠ACB的度数,再根据线段垂直平分线的性质可得BF=CF,进而可得∠FCB=24°,然后可算出∠ACF的度数.
【解答】解:∵BD平分∠ABC,
∴∠DBC=∠ABD=24°,
 ∵∠A=60°,
∵∠A=60°,
∴∠ACB=180°﹣60°﹣24°×2=72°,
∵BC的中垂线交BC于点E,
∴BF=CF,
∴∠FCB=24°,
∴∠ACF=72°﹣24°=48°,
故选:A.
【点评】此题主要考查了线段垂直平分线的性质,以及三角形内角和定理,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
随着电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.000 000 74mm2,这个数用科学记数法表示为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
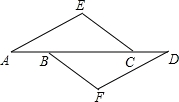
如图,在△AEC和△DFB中,∠E=∠F,点A、B、C、D在同一直线上,有如下三个关系式:①AE∥DF,②AB=CD,③CE=BF.
(1)请用其中两个关系式作为条件,另一个作为结论,写出你认为正确的所有命题(用序号写出命题书写形式:“如果⊗、⊗,那么⊗”)
(2)选择(1)中你写出的一个命题,说明它正确的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
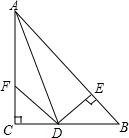
如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB;
(2)AB=AC+CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知(﹣2,y1),(﹣1.5,y2),(1,y3)是直线y=2x+b(b为常数)上的三个点,则y1,y2,y3的大小关系是__________.(用“>”表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( )

A.4对 B.3对 C.2对 D.1对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com