
【题目】如图,在正方形ABCD中,E、F分别为AB、BC的中点,连接CE、DF,将△CBE沿CE对折,得到△CGE,延长EG交CD的延长线于点H。

(1)求证:CE⊥DF;
(2)求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)运用△BCE≌Rt△CDF(SAS),再利用角的关系求得∠CKD=90°即可解题.
(2)设正方形ABCD的边长为2a,设CH=x,利用勾股定理求出a与x之间的关系即可解决问题.
(1)证明:设EC交DF于K.
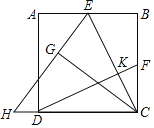
∵E,F分别是正方形ABCD边AB,BC的中点,
∴CF=BE,
在Rt△BCE和Rt△CDF中,
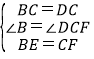 ,
,
∴△BCE≌Rt△CDF(SAS),
∠BCE=∠CDF,
又∵∠BCE+∠ECD=90°,
∴∠CDF+∠ECD=90°,
∴∠CKD=90°,
∴CE⊥DF.
(2)解:设正方形ABCD的边长为2a.
EB=EG,∠BEC=∠CEG,∠EGC=∠B=90°
∵CD∥AB,
∴∠ECH=∠BEC,∴∠ECH=∠CEH,
∴EH=CH,
∵BE=EG=a,CD=CG=2a,
在Rt△CGH中,设CH=x,
∴x2=(x-a)2+(2a)2,
∴x=![]() a,
a,
∴GH=EH-EG=![]() a-a=
a-a=![]() a,
a,
∴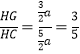 .
.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】阅读理解题:
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1,依次类推,排在第n位的数称为第n项,记为an.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).如:数列1,3,9,27,…为等比数列,其中a1=1,公比为q=3.
则:(1)等比数列3,6,12,…的公比q为 ,第4项是 .
(2)如果一个数列a1,a2,a3,a3,…是等比数列,且公比为q,那么根据定义可得到:
![]() ,……
,…… ![]() .
.
∴a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q= a1q3,……
由此可得:an= (用a1和q的代数式表示)
(3)若一等比数列的公比q=2,第2项是10,请求它的第1项与第4项.
查看答案和解析>>
科目:初中数学 来源: 题型:
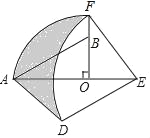
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x人.
(1)求第一轮后患病的人数;(用含x的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
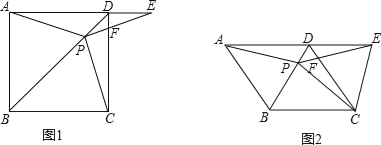
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在数轴上表示下列各数,并用“<”号把它们连接.
3, -1, 0, -2.5, 1.5, 2![]()
(2)快递员要从物流中心出发送货,已知甲住户在物流中心的东边 2km 处,乙住户在甲住户的西边 3km 处,丙住户在物流中心的西边 1.5km 处,请建立数轴表示物流中心、甲住户、乙住户、丙住户的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与反比例函数
与反比例函数![]() (
(![]() )图像交于点A,将直线向右平移4个单位,交反比例函数
)图像交于点A,将直线向右平移4个单位,交反比例函数![]() (
(![]() )图像于点B,交y轴于点C,连结AB、AC,则△ABC的面积为_______.
)图像于点B,交y轴于点C,连结AB、AC,则△ABC的面积为_______.
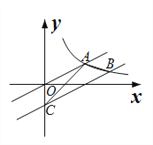
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
幻方的历史很悠久,传说中最早出现在夏禹时代的“洛书”,用今天的数学符号翻译出来,就是一个三阶幻方,即将若干个数组成一个正方形数阵,任意一行、一列及对角线上的数字之和都相等.如图1,就是一个三阶幻方,由1,2,3,4,5,6,7,8,9九个数字组成的一个三行三列的矩阵(如图),其对角线、横行、纵向的和都为15.
(1)探究:研究发现三阶幻方中间的数字与9个数的和有确定的数量关系.如果设数字连续性三阶幻方中间的数字是a,则幻方中9个数字之和是 (用含a的字母代数式表示)
(2)应用:请你选取一组数据构造一个三阶幻方,填入到如图2的3×3方格中,使得每行、每列、每条对角线上的三个数之和都等于21;


(3)拓展:
数阵是由幻方演化出来的另一种数字图.将连续的奇数1,3,5,7,9…排列成数阵(如图3),用十字框随机框出5个数,十字框中的五数之和能等于2020吗?并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com