Question

【题目】如图，OB、OC是内部的两条射线, OM平分，ON平分.

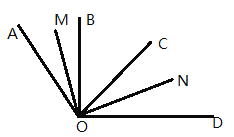
（1）若，求的度数；

（2）若，求的度数（用含的代数式表示）

Answer 1

【答案】（1）120°（2）（160x）°

【解析】

（1）利用角平分线的定义可得∠AOM＝∠BOM，∠DON＝∠CON，易得∠BOM＋∠CON＝∠AOM＋∠DON，利用∠MON∠BOC＝∠BOM＋∠CON，可得结果；

（2）由角的加减可得∠AOM＋∠DON，易得∠BOM＋∠CON，再利用∠BOC＝∠MON（∠BOM＋∠CON）可得结果．

（1）∵∠MON∠BOC＝∠BOM＋∠CON，∠BOC＝40°，∠MON＝80°，

∴∠BOM＋∠CON＝80°40°＝40°，

∵OM平分∠AOB，ON平分∠COD，

∴∠AOM＝∠BOM，∠DON＝∠CON，

∴∠AOM＋∠DON＝40°，

∴∠AOD＝∠MON＋∠AOM＋∠DON＝80°＋40°＝120°；

（2）∵∠AOD＝x°，∠MON＝80°，

∴∠AOM＋∠DON＝∠AOD∠MON＝（x80）°，

∵∠BOM＋∠CON＝∠AOM＋∠DON＝（x80）°，

∴∠BOC＝∠MON（∠BOM＋∠CON）＝80°（x80）°＝（160x）°.