
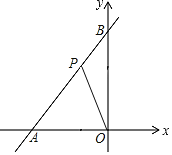
【题目】如图,一次函数y=![]() x+4与x轴、y轴分别交于点A和点B,在线段AB上有一动点P(不与点A、B重合),连接OP,当点P的坐标为_____时线段OP最短.
x+4与x轴、y轴分别交于点A和点B,在线段AB上有一动点P(不与点A、B重合),连接OP,当点P的坐标为_____时线段OP最短.
【答案】(﹣![]() ,
,![]() )
)
【解析】
过点O作OP⊥AB于点P,此时OP最短,过点P作PE⊥x轴于点E,利用一次函数图象上点的坐标特征、勾股定理及三角形的面积,可求出OP的长,在Rt△AOP中利用勾股定理可求出AP的长,由PE∥BO可得出△APE∽△ABO,利用相似三角形的性质可求出AE,PE的长,结合OE=OA﹣AE可求出OE的长,结合点P所在的象限即可得出点P的坐标,此题得解.
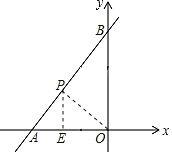
解:过点O作OP⊥AB于点P,此时OP最短,过点P作PE⊥x轴于点E,如图所示.
当x=0时,y=![]() x+4=4,
x+4=4,
∴点B的坐标为(0,4);
当y=0时,![]() x+4=0,
x+4=0,
解得:x=﹣3,
∴点A的坐标为(﹣3,0).
∴AB=![]() =5,
=5,
∴OP=![]() =
=![]() ,
,
∴AP=![]() =
=![]() .
.
∵PE∥BO,
∴△APE∽△ABO,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴![]() ,
,
∴OE=OA﹣AE=3﹣![]() ,
,
∴点P的坐标为![]() .
.
故答案为:![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC,AD的中点,连接AE、CF.
(1)求证:四边形AECF是矩形;
(2)若AB=2,求菱形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=5cm,BC=13cm,点D在线段AC上,且CD=7cm,动点P从距B点15cm的E点出发,以每秒2cm的速度沿射线EA的方向运动,时间为t秒.
(1)求AD的长.
(2)用含有t的代数式表示AP的长.
(3)在运动过程中,是否存在某个时刻,使△ABC与△ADP全等?若存在,请求出t值;若不存在,请说明理由.
(4)直接写出t=______秒时,△PBC为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为8等边三角形,如图所示,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为每秒1个单位长度,点N的运度为每秒2个单位长度,当点M第一次到达B点时,M、N同时停止运动.

(1)点M、N运动几秒后,可得到等边三角形![]() ?
?
(2)点M、N运动几秒后,M、N两点重合?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰![]() ?如存在,请求出此时M、N运动的时间.
?如存在,请求出此时M、N运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A﹣∠B=∠C
B.∠A:∠B:∠C=3:4:5
C.(b+c)(b﹣c)=a2
D.a=7,b=24,c=25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时开始修筑,施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通,下图是甲、乙两个工程队修道路长度y(米)与修筑时间x(天)之间的函数图象,请根据图象所提供的信息,解答下列问题:
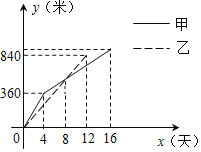
(1)写出乙工程队修道路的长度y与修筑时间x之间的函数关系式:_____;
(2)甲工程队前8天所修公路为_____米,该公路的总长度为_____米;
(3)若乙工程队不提前离开,则两队只需_____天就能完成任务;
(4)甲、乙两工程队第_____天时所修道路的长度相差80米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过第2011次运动后,动点P的坐标是( )
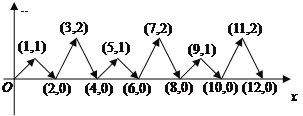
A.(2011,0)B.(2011,1)C.(2011,2)D.(2010,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
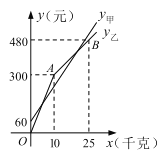
(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
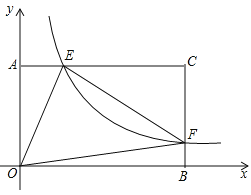
【题目】在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴建立如图所示的平面直角坐标系,F是BC上的一个动点(不与B、C重合),过F点的反比例函数![]() (k>0)的图象与AC边交于点E,连接OE,OF,EF.
(k>0)的图象与AC边交于点E,连接OE,OF,EF.
(1)若tan∠BOF=![]() ,求F点的坐标;
,求F点的坐标;
(2)当点F在BC上移动时,△OEF与△ECF的面积差记为S,求当k为何值时,S有最大值,最大值是多少?
(3)是否存在这样的点F,使得△OEF为直角三角形?若存在,求出此时点F坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com