
【题目】已知等腰直角![]() ,
,![]() ,
,![]() ,
,![]() 为边
为边![]() 上一动点,连结
上一动点,连结![]() ,在射线
,在射线![]() 上取一点
上取一点![]() 使
使![]() ,若点
,若点![]() 由
由![]() 运动到
运动到![]() ,则点
,则点![]() 运动的路径长为_______.
运动的路径长为_______.
【答案】![]()
【解析】
由已知可得△BAD∽△BEA,再结合△ACB是等腰直角三角形,可得∠BEA=45°,以C为圆心,CA为半径画弧交BC延长线于M,根据∠AEB=![]() ∠ACB,可得点E一定落在以C为圆心,CA为半径的圆弧上,即可推出点D由A运动到C,点E走过的路径为弧AM,即可得到答案.
∠ACB,可得点E一定落在以C为圆心,CA为半径的圆弧上,即可推出点D由A运动到C,点E走过的路径为弧AM,即可得到答案.
如图:
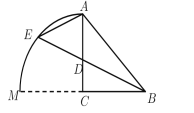
∵AB2=BE·BD,
∴![]() ,
,
∵∠ABD=∠EBA,
∴△BAD∽△BEA,
∴∠BAD=∠BEA,
∵△ACB是等腰直角三角形,
∴∠CAB=45°,
∴∠BEA=45°,
以C为圆心,CA为半径画弧交BC延长线于M,
∵∠AEB=![]() ∠ACB,
∠ACB,
∴点E一定落在以C为圆心,CA为半径的圆弧上,
当D与A重合时,E与A重合,
当D与C重合时,E与M重合,
即点D由A运动到C,点E走过的路径为弧AM,
∴弧AM=![]() =
=![]() ,
,
故点E运动的路径长为π,
故答案为:π.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c经过(﹣1,0),(0,﹣3),(2,3)三点.
(1)求这条抛物线的表达式;
(2)写出抛物线的开口方向、对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节期间,红星商场举行抽奖促销活动,凡在本商场购物总金额在300元以上者,均可抽一次奖,奖品为精美小礼品.抽奖办法是:在一个不透明的袋子中装有四个标号分别为1,2,3,4的小球,它们的形状、大小、质地等完全相同.抽奖者第一次摸出一个小球,不放回,第二次再摸出一个小球,若两次摸出的小球中有一个小球标号为“1”,则获奖.
(1)请你用树形图或列表法表示出抽奖所有可能出现的结果;
(2)求抽奖人员获奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,某小区计划购买甲、乙两种品牌的消毒剂,乙品牌消毒剂每瓶的价格比甲品牌消毒剂每瓶价格的3倍少50元,已知用300元购买甲品牌消毒剂的数量与用400元购买乙品牌消毒剂的数量相同.
(1)求甲、乙两种品牌消毒剂每瓶的价格各是多少元?
(2)若该小区从超市一次性购买甲、乙两种品牌的消毒剂共40瓶,且总费用为1400元,求购买了多少瓶乙品牌消毒剂?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程y(米)与时间x(分)的函数关系如图2所示.
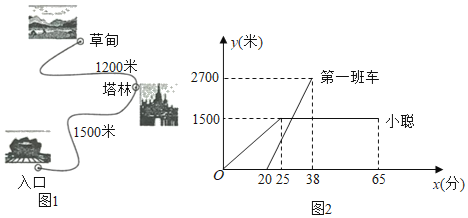
(1)求第一班车离入口处的路程y(米)与时间x(分)函数表达式.并写出x的取值范围;
(2)求第一班车从入口处到达塔林所需的时间;
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般地,对于已知一次函数y1=ax+b,y2=cx+d(其中a,b,c,d为常数,且ac<0),定义一个新函数y=![]() ,称y是y1与y2的算术中项,y是x的算术中项函数.
,称y是y1与y2的算术中项,y是x的算术中项函数.
(1)如:一次函数y1=![]() x﹣4,y2=﹣
x﹣4,y2=﹣![]() x+6,y是x的算术中项函数,即y=
x+6,y是x的算术中项函数,即y= .
.
①自变量x的取值范围是 ,当x= 时,y有最大值;
②根据函数研究的途径与方法,请填写下表,并在图1中描点、连线,画出此函数的大致图象;
x | 8 | 9 | 10 | 12 | 13 | 14 | 16 | 17 | 18 |
y | 0 | 1.2 | 1.6 |
| 2.04 | 2 |
| 1.2 | 0 |

③请写出一条此函数可能有的性质 ;
(2)如图2,已知一次函数y1=![]() x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y=
x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y= .
.
①判断:点A、C、E是否在此算术中项函数的图象上;
②在平面直角坐标系中是否存在一点,到此算术中项函数图象上所有点的距离相等,如果存在,请求出这个点;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 为
为![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 上一点,连接
上一点,连接![]() 并延长
并延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
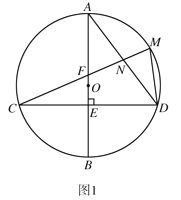
(1)如图1,连接![]() .求证:
.求证:![]() ;
;
(2)如图2,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 延长线于点
延长线于点![]() 求证:
求证:![]() .
.
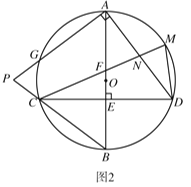
(3)如图3,在(2)的条件下,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
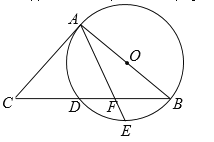
【题目】如图,AB是⊙O的直径, BC交⊙O于点D,E是![]() 的中点,连接AE交BC于点F,∠ACB =2∠EAB.
的中点,连接AE交BC于点F,∠ACB =2∠EAB.
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)若![]() ,
,![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
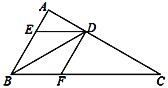
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
⑴求证:四边形BEDF为菱形;
⑵如果∠A=100°,∠C=30°,求∠BDE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com