
【题目】一般地,对于已知一次函数y1=ax+b,y2=cx+d(其中a,b,c,d为常数,且ac<0),定义一个新函数y=![]() ,称y是y1与y2的算术中项,y是x的算术中项函数.
,称y是y1与y2的算术中项,y是x的算术中项函数.
(1)如:一次函数y1=![]() x﹣4,y2=﹣
x﹣4,y2=﹣![]() x+6,y是x的算术中项函数,即y=
x+6,y是x的算术中项函数,即y= .
.
①自变量x的取值范围是 ,当x= 时,y有最大值;
②根据函数研究的途径与方法,请填写下表,并在图1中描点、连线,画出此函数的大致图象;
x | 8 | 9 | 10 | 12 | 13 | 14 | 16 | 17 | 18 |
y | 0 | 1.2 | 1.6 |
| 2.04 | 2 |
| 1.2 | 0 |

③请写出一条此函数可能有的性质 ;
(2)如图2,已知一次函数y1=![]() x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y=
x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y= .
.
①判断:点A、C、E是否在此算术中项函数的图象上;
②在平面直角坐标系中是否存在一点,到此算术中项函数图象上所有点的距离相等,如果存在,请求出这个点;如果不存在,请说明理由.
【答案】①8≤x≤18,13;②2,1.7,画图见解析;③8<x<13时,y随x的增大而增大和13<x<18时,y随x的增大而减小(答案不唯一);(2)①点A、C、E在此算术中项函数的图象上;②存在,(﹣![]() ,0)
,0)
【解析】
(1)①转化为二次不等式求出c的取值范围,利用二次函数的性质求出最大值.
②把x=12,x=16代入函数解析式求函数值即可,利用描点法画出函数图象即可.
③观察函数图象,写出函数的性质即可.
(2)①求出A,C,E的坐标,利用待定系数法判断即可.
②不存在,首先根据A,E,C确定这个点的坐标,然后取x=0,求出算术中项函数图象上的点的坐标验证即可.
解:(1)①由题意(![]() x﹣4)(﹣
x﹣4)(﹣![]() x+6)≥0,
x+6)≥0,
解得8≤x≤18,
∵y=![]() ,
,
∵﹣![]() <0,
<0,
∴x=13时,y有最大值,最大值为![]() .
.
故答案为8≤x≤18,13.
②x=12时,y=![]() =2,
=2,
x=16时,y=![]() ≈1.7
≈1.7
故答案为2,1.7.
函数图象如图所示:

③性质:8<x<13时,y随x的增大而增大和13<x<18时,y随x的增大而减小;
故答案为:8<x<13时,y随x的增大而增大和13<x<18时,y随x的增大而减小(答案不唯一);
(2)①由题意E(![]() ,
,![]() ),A(﹣4,0),C(3,0),
),A(﹣4,0),C(3,0),
对于函数y= ,
,
当x=![]() 时,y=
时,y=![]() ,
,
∴点E在这个函数的图象上,
当x=﹣4时,y=0,
∴点A在这个函数的图象上,
当x=3时,y=0,
∴点C在这个函数的图象上.
②不存在,由图2可知,∵AE⊥EC,
∴∠AEC=90°,
到A,C,E距离相等的点是AC的中点T(﹣![]() ,0),这个距离是3.5,
,0),这个距离是3.5,
∵算术中项函数图象上的点P[x, ],
],
PT= ,
,
∴存在这样的点(﹣![]() ,0)到此算术中项函数图象上所有点的距离相等.
,0)到此算术中项函数图象上所有点的距离相等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB,如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
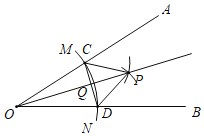
A.CP∥OBB.CP=2QCC.∠AOP=∠BOPD.CD⊥OP
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)则样本容量是 ,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李辉到服装专卖店去做社会调查,了解到商店为了激励营业员的工作积极性实行了“月总收入=基本工资+计件奖金”的方法,并获得了如下信息:
营业员 | 嘉琪 | 嘉善 |
月销售件数/件 | 400 | 300 |
月总收入/元 | 7800 | 6600 |
假设月销售件数为x件,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)求a、b的值.
(2)若营业员嘉善某月总收入不低于4200元,那么嘉善当月至少要卖多少件衣服?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定学生平均每天户外活动的时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次调查中,一共调查了多少名学生?
(2)本次调查中,户外活动时间为0.5小时的学生有多少名?并补全下面的两幅统计图;
(3)如果某校共有1200名学生,请你估计该校学生中户外活动时间为2小时的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:
,下列结论:![]() ;
;![]() >0;(3)若点
>0;(3)若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
;![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() 其中正确的结论是______.
其中正确的结论是______.
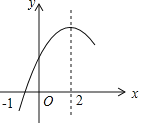
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】像![]() =x这样的方程,可以通过方程两边平方把它转化为2x+3=x2,解得x1=3,x2=﹣1.但由于两边平方,可能产生增根,所以需要检验,经检验,当x1=3时,
=x这样的方程,可以通过方程两边平方把它转化为2x+3=x2,解得x1=3,x2=﹣1.但由于两边平方,可能产生增根,所以需要检验,经检验,当x1=3时,![]() =3满足题意;当x2=﹣1时,
=3满足题意;当x2=﹣1时,![]() =﹣1不符合题意;所以原方程的解是x=3.运用以上经验,则方程x+
=﹣1不符合题意;所以原方程的解是x=3.运用以上经验,则方程x+![]() =1的解为_____.
=1的解为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com