
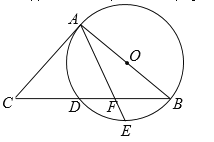
【题目】如图,AB是⊙O的直径, BC交⊙O于点D,E是![]() 的中点,连接AE交BC于点F,∠ACB =2∠EAB.
的中点,连接AE交BC于点F,∠ACB =2∠EAB.
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)若![]() ,
,![]() ,求BF的长.
,求BF的长.
【答案】(1)AC是⊙O的切线,见解析;(2)![]()
【解析】
(1)首先证明∠ACB =∠BAD,然后根据圆周角定理的推论得出∠ACB +∠CAD=90°,则有∠BAD+∠CAD=90°,所以BA⊥AC,则可证明AC是⊙O的切线;
(2)过点F做FH⊥AB于点H.首先通过角平分线的性质得出FH=FD,且FH∥AC,然后利用锐角三角函数求出CD,BD的长度,然后设 DF=x,则FH=x,![]() ,最后利用
,最后利用![]() 建立关于x的方程,解方程即可得出答案.
建立关于x的方程,解方程即可得出答案.
解:(1)AC是⊙O的切线
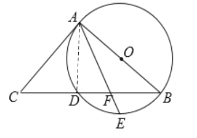
理由:如图,连接AD.
∵ E是![]() 中点,
中点,
∴![]() .
.
∴ ∠DAE=∠EAB.
∵ ∠ACB =2∠EAB,
∴∠ACB =∠BAD.
∵ AB是⊙O的直径,
∴ ∠ADB=∠ADC=90°,
∴ ∠ACB +∠CAD=90°,
∴ ∠BAD+∠CAD=90°.
即 BA⊥AC.
∴ AC是⊙O的切线.
(2)解:如图,过点F做FH⊥AB于点H.

∵ AD⊥BD,FH⊥AB,∠DAE=∠EAB,
∴ FH=FD,且FH∥AC.
在Rt△ADC中,
∵![]() ,
,![]() ,
,
∴ CD=6.
同理,在Rt△BAC中,可求得![]() .
.
∴![]() .
.
设 DF=x,则FH=x,![]() .
.
∵ FH∥AC,
∴ ∠BFH=∠ACB.
∴![]() .
.
即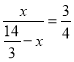 .
.
解得x=2,
经检验,x=2是原分式方程的解,
∴![]() .
.


科目:初中数学 来源: 题型:
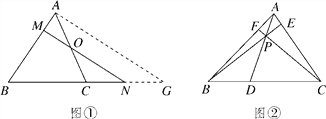
【题目】如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.
【问题引入】
(1)若点O是AC的中点, ![]() ,求
,求![]() 的值;
的值;
温馨提示:过点A作MN的平行线交BN的延长线于点G.
【探索研究】
(2)若点O是AC上任意一点(不与A,C重合),求证: ![]() ;
;
【拓展应用】
(3)如图②所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F.若![]() ,
, ![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:
,下列结论:![]() ;
;![]() >0;(3)若点
>0;(3)若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
;![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() 其中正确的结论是______.
其中正确的结论是______.
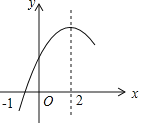
查看答案和解析>>
科目:初中数学 来源: 题型:
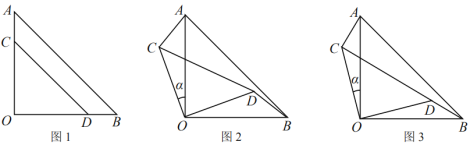
【题目】两块等腰直角三角形纸片AOB和COD 按图1所示放置,直角顶点重合在点O处,其中AB=3![]() ,CD=6.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°),如图2所示.当BD与CD在同一直线上(如图3)时,tanα的值等于( )
,CD=6.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°),如图2所示.当BD与CD在同一直线上(如图3)时,tanα的值等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,

(1)证明:Rt△ABM ∽Rt△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
(3)当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
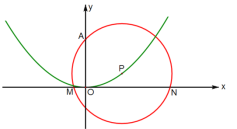
【题目】如图,抛物线y=ax2+bx+c(a、b、c是常数,a≠0)经过原点O和![]() 两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0, 2).
两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0, 2).
(1)a= ,b= ,c= ;
(2)求证:在点P运动的过程中,⊙P始终与x轴相交;
(3)设⊙P与x轴相交于M、N两点,M在N的左边.当△AMN为等腰三角形时,直接写出圆心P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )
A.2种B.3种C.4种D.5种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com