【题目】二次函数y=x2+bx图象的对称轴为直线x=1，若关于x的一元二次方程x2+bx﹣t=0（t为实数）在﹣1≤x≤2的范围内有解，则t的取值范围是_____．
【答案】﹣1≤t≤3．
【解析】
利用抛物线的对称轴方程求出b的值得到抛物线解析式为y=x2-2x，再利用配方法得到抛物线的顶点坐标为（1，-1），然后利用当抛物线y=x2-2x与直线y=t在-1≤x≤2有交点确定t的范围．
∵二次函数y=x2+bx图象的对称轴为直线x=1，
∴-
=1，解得b=-2，
∴抛物线解析式为y=x2-2x，
∵y=（x-1）2-1，
∴抛物线的顶点坐标为（1，-1），
当抛物线y=x2-2x与直线y=t在-1≤x≤2有交点时，关于x的一元二次方程x2+bx-t=0（t为实数）在-1≤x≤2的范围内有解，
而-1≤x≤2对应的二次函数值y的范围为-1≤y≤3，
所以t的范围为-1≤t≤3．
故答案为-1≤t≤3．
科目：初中数学 来源： 题型：
【题目】如图，直线y＝k1x＋b与双曲线y＝
相交于A(1,2)、B(m，－1)两点．
(1)求直线和双曲线的解析式；
(2)若A1(x1，y1)、A2(x2，y2)、A3(x3，y3)为双曲线上的三点，且x1＜x2＜0＜x3，请直接写出y1、y2、y3的大小关系式；
(3)观察图象，请直接写出不等式k1x＋b＞的解集．
查看答案和解析>>
科目：初中数学 来源： 题型：
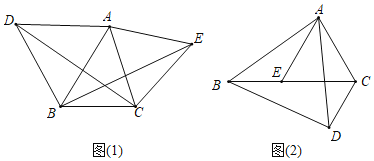
【题目】（1）感知：如图（1），在△ABC中，分别以AB、AC为边在△ABC外部作等边三角形△ABD、△ACE，连接CD、BE．求证：BE＝DC；
（2）应用：如图（2），在△ABC中，AB＞AC，分别以AB、AC为边在△ABC内部作等腰三角形△ABD、△ACE，点E恰好在BC边上，使AB＝AD，AC＝AE，且∠BAD＝∠CAE，连接CD，CE＝3cm，CD＝2cm，△ABC的面积为25cm2，求△ABE的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于抛物线
.
（1）它与x轴交点的坐标为 ，与y轴交点的坐标为 ，顶点坐标为 ；
（2）在坐标系中利用描点法画出此抛物线；
x | … | … | |||||
y | … | … |
（3）利用以上信息解答下列问题：若关于x的一元二次方程
（t为实数）在
＜x＜
的范围内有解，则t的取值范围是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，定义点P（x，y）的变换点为P′（x+y，x﹣y）．
（1）如图1，如果⊙O的半径为
，
①请你判断M（2，0），N（﹣2，﹣1）两个点的变换点与⊙O的位置关系；
②若点P在直线y=x+2上，点P的变换点P′在⊙O的内，求点P横坐标的取值范围．
（2）如图2，如果⊙O的半径为1，且P的变换点P′在直线y=﹣2x+6上，求点P与⊙O上任意一点距离的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解
如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重复部分；…；将余下部分沿∠BnAnC的平分线AnBn+1折叠，点Bn与点C重合，无论折叠多少次，只要最后一次恰好重合，∠BAC是△ABC的好角．
小丽展示了确定∠BAC是△ABC的好角的两种情形．情形一：如图2，沿等腰三角形ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合．
探究发现
△ABC中，∠B=2∠C，经过两次折叠，∠BAC是不是△ABC的好角？ （填“是”或“不是”）．
小丽经过三次折叠发现了∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为 ．
根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为 ．
应用提升
（3）小丽找到一个三角形，三个角分别为15°、60°、105°，发现60°和105°的两个角都是此三角形的好角．
请你完成，如果一个三角形的最小角是4°，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等边△ABC的边长为2，AD是BC边上的中线，M是AD上的动点，E是边AC的中点，则EM+CM的最小值为( )
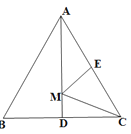
A.1B.12 C.3 D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
