
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论:①∠BAD=∠CAD; ②AD上任意一点到AB,AC的距离相等;
③BD=CD; ④若点P在直线AD上,则PB=PC.其中正确的是( )
A.①
B.①②
C.①②③
D.①②③④
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】已知点P在第二象限,且到x轴的距离为3,到y轴的距离为5,则点P的坐标为( )
A.(-5,3)B.(3,5)C.(-3,-5)D.(5,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D,E在BC上,连接AD,AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )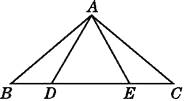
A.BD=CE
B.AD=AE
C.DA=DE
D.BE=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:如图1,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP、BP,求AP+![]() BP的最小值.
BP的最小值.
(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图2,连接CP,在CB上取点D,使CD=1,则有![]() ,又∵∠PCD=∠BCP,∴△PCD∽△BCP.∴
,又∵∠PCD=∠BCP,∴△PCD∽△BCP.∴![]() ,∴PD=
,∴PD=![]() BP,∴AP+
BP,∴AP+![]() BP=AP+PD.
BP=AP+PD.
请你完成余下的思考,并直接写出答案:AP+![]() BP的最小值为 .
BP的最小值为 .
(2)自主探索:在“问题提出”的条件不变的情况下, ![]() AP+BP的最小值为 .
AP+BP的最小值为 .
(3)拓展延伸:已知扇形COD中,∠COD=90°,OC=6,OA=3,OB=5,点P是![]() 上一点,求2PA+PB的最小值.
上一点,求2PA+PB的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
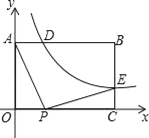
【题目】如图,已知矩形OABC中,OA=3,AB=4,双曲线y=![]() (k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD
(k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD
(1)求k的值和点E的坐标;
(2)点P是线段OC上的一个动点,是否存在点P,使∠APE=90°?若存在,求出此时点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a1+a2=1,a2+a3=2,a3+a4=3,…,a99+a100=99,a100+a1=100,那么a1+a2+a3+…a100= 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com