
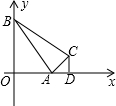
 如图,△ABC各顶点的坐标分别为A(3,0)、B(0,4)、C(4,2),过点C作CD⊥x轴,垂足为D.求证:△ACD∽△ABC.
如图,△ABC各顶点的坐标分别为A(3,0)、B(0,4)、C(4,2),过点C作CD⊥x轴,垂足为D.求证:△ACD∽△ABC. 分析 先根据两点间的距离公式计算出AB=5,BC=2$\sqrt{5}$,AC=$\sqrt{5}$,再得到AD=1,CD=2,然后得到:$\frac{AB}{AC}=\frac{BC}{CD}=\frac{AC}{AD}$=$\sqrt{5}$,则可根据三组对应边的比相等的两个三角形相似得到结论.
解答 证明:如图,∵A(3,0),B(0,4),C(4,2),
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,BC=$\sqrt{{4}^{2}+(4-2)^{2}}$=2$\sqrt{5}$,AC=$\sqrt{(3-4)^{2}+{2}^{2}}$=$\sqrt{5}$,
∵CD⊥x轴,
∴AD=4-3=1,CD=2,
∵$\frac{AB}{AC}$=$\frac{5}{\sqrt{5}}$=$\sqrt{5}$,$\frac{BC}{CD}$=$\frac{2\sqrt{5}}{2}$=$\sqrt{5}$,$\frac{AC}{AD}$=$\frac{\sqrt{5}}{1}$=$\sqrt{5}$,
∴$\frac{AB}{AC}$=$\frac{BC}{CD}$=$\frac{AC}{AD}$,
∴△ABC∽△ACD.
点评 本题考查了相似三角形的判定:三组对应边的比相等的两个三角形相似.会利用两点间的距离公式计算线段的长.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 各有一个角为40°的两等腰三角形 | |
| B. | 有两边之比都为2:3的两直角三角形 | |
| C. | 有两边及其中一边上的高对应成比例的两三角形 | |
| D. | 两边及两边夹角的平分线对应成比例的两三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
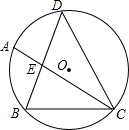 如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E,
如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com