
分析 (1)约分计算即可求解;
(2)①先算括号里面的减法,再约分计算即可求解;
②根据题意列出算式2012×(1-$\frac{1}{2}$)×(1-$\frac{1}{3}$)×…×(1-$\frac{1}{2012}$),再先算括号里面的减法,再约分计算即可求解.
解答 解:(1)猜想:$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}…×\frac{n}{n+1}$=$\frac{1}{n+1}$;
(2)①($\frac{1}{100}-1$)×($\frac{1}{99}-1$)×($\frac{1}{98}-1$)×…×($\frac{1}{4}-1$)×($\frac{1}{3}-1$)×($\frac{1}{2}-1$)
=$\frac{99}{100}$×$\frac{98}{99}$×$\frac{97}{98}$×…×$\frac{3}{4}$×$\frac{2}{3}$×$\frac{1}{2}$
=$\frac{1}{100}$;
②依题意有
2012×(1-$\frac{1}{2}$)×(1-$\frac{1}{3}$)×…×(1-$\frac{1}{2012}$)
=2012×$\frac{1}{2}$×$\frac{2}{3}$×…×$\frac{2011}{2012}$
=1.
故答案为:$\frac{1}{n+1}$;$\frac{1}{100}$.
点评 此题考查了有理数的混合运算,第(3)问根据题意列出算式是解本题的关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 11+[(-13)+7]=17 | B. | (-2.5)+[5+(-2.5)]=5 | C. | [3$\frac{1}{2}$+(-3$\frac{1}{2}$)]+(-2)=-2 | D. | 3.14+[(-4)+3.14]=-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若两数的差为0,则这两数必相等 | |
| B. | 较大的数减去较小的数,差一定是正数 | |
| C. | 两数之差一定小于被减数 | |
| D. | 减去一个负数,差一定大于被减数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
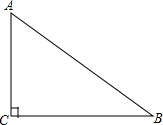 如图,在△ABC中,∠C=90°,用直尺和圆规作BC的垂直平分线l,交斜边AB于点O.
如图,在△ABC中,∠C=90°,用直尺和圆规作BC的垂直平分线l,交斜边AB于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com