
【题目】在△ABC中,AB=1,BC=2,以AC为边作等边三角形ACD,连接BD,则线段BD的最大值为_____.
科目:初中数学 来源: 题型:
【题目】已知x1,x2是关于x的一元二次方程4kx2﹣4kx+k+1=0的两个实数根.
(1)是否存在实数k,使(2x1﹣x2)(x1﹣2x2)=﹣![]() 成立?若存在,求出k的值;若不存在,说明理由;
成立?若存在,求出k的值;若不存在,说明理由;
(2)求使![]() ﹣2的值为整数的实数k的整数值;
﹣2的值为整数的实数k的整数值;
(3)若k=﹣2,λ=![]() ,试求λ的值.
,试求λ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
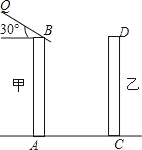
【题目】如图,是住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=30m,现需了解甲楼对乙楼的采光的影响情况.
(1)当太阳光与水平线的夹角为30°角时,求甲楼的影子在乙楼上有多高(精确到0.1m,![]() =1.73);
=1.73);
(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把三角形纸片![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在四边形
落在四边形![]() 内部点
内部点![]() 处,
处,
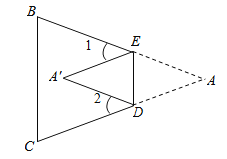
(1)写出图中一对全等的三角形,井写出它们的所有对应角.
(2)设![]() 的度数为
的度数为![]() ,
,![]() 的度数为
的度数为![]() ,那么
,那么![]() 的度数分别是多少(用含
的度数分别是多少(用含![]() 或
或![]() 的式子表示)?
的式子表示)?
(3)![]() 与
与![]() 之间有一种数量关系始终保持不变,请找出这个规律,井说明理由.
之间有一种数量关系始终保持不变,请找出这个规律,井说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为边BC的中点,四边形ABDE是平行四边形,AC,DE相交于点O.
(1)求证:四边形ADCE是矩形;
(2)若∠AOE=60°,AE=2,求矩形ADCE对角线的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂要把一批产品从A地运往B地,若通过铁路运输,则每千米需交运费15元,还要交装卸费400元及手续费200元,若通过公路运输,则每千米需要交运费25元,还需交手续费100元(由于本厂职工装卸,不需交装卸费).设A地到B地的路程为x km,通过铁路运输和通过公路运输需交总运费y1元和y2元,
(1)求y1和y2关于x的表达式.
(2)若A地到B地的路程为120km,哪种运输可以节省总运费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC,BD交于点O,AG平分∠BAC交BD于G,DE⊥AG于点H.下列结论:①AD=2AE:②FD=AG;③CF=CD:④四边形FGEA是菱形;⑤OF=![]() BE,正确的有( )
BE,正确的有( )
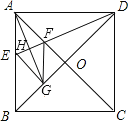
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
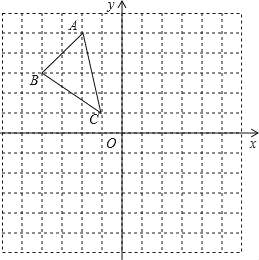
【题目】在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣4,3),C(﹣1,1).写出各点关于原点的对称点的坐标_____,_____,_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com