
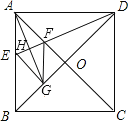
【题目】如图,在正方形ABCD中,对角线AC,BD交于点O,AG平分∠BAC交BD于G,DE⊥AG于点H.下列结论:①AD=2AE:②FD=AG;③CF=CD:④四边形FGEA是菱形;⑤OF=![]() BE,正确的有( )
BE,正确的有( )
A.2个B.3个C.4个D.5个
【答案】C
【解析】
①根据正方形的性质和角平分线的定义得:∠BAG=∠CAG=22.5°,由垂直的定义计算∠AED=90°﹣22.5°=67.5°,∠EDA=∠EDG=22.5°,得ED是AG的垂直平分线,则AE=EG,△BEG是等腰直角三角形,则AD=AB>2AE,可作判断;②证明△DAF≌△ABG(ASA),可作判断;③分别计算∠CDF=∠CFD=67.5°,可作判断;④根据对角线互相平分且垂直的四边形是菱形可作判断;⑤设BG=x,则AF=AE=x,表示OF和BE的长,可作判断.
解:①∵四边形ABCD是正方形,
∴∠BAD=90°,∠BAC=45°,
∵AG平分∠BAC,
∴∠BAG=∠CAG=22.5°,
∵AG⊥ED,
∴∠AHE=∠EHG=90°,
∴∠AED=90°﹣22.5°=67.5°,
∴∠ADE=22.5°,
∵∠ADB=45°,
∴∠EDG=22.5°=∠ADE,
∵∠AHD=∠GHD=90°,
∴∠DAG=∠DGA,
∴AD=DG,AH=GH,
∴ED是AG的垂直平分线,
∴AE=EG,
∴∠EAG=∠AGE=22.5°,
∴∠BEG=45°=∠ABG,
∴∠BGE=90°,
∴AE=EG<BE,
∴AD=AB>2AE,
故①不正确;
②∵四边形ABCD是正方形,
∴AD=AB,∠DAF=∠ABG=45°,
∵∠ADF=∠BAG=22.5°,
∴△DAF≌△ABG(ASA),
∴DF=AG,
故②正确;
③∵∠CDF=45°+22.5°=67.5°,∠CFD=∠AFE=90°﹣22.5°=67.5°,
∴∠CDF=∠CFD,
∴CF=CD,
故③正确;
④∵∠EAH=∠FAH,∠AHE=∠AHF,
∴∠AEF=∠AFE,
∴AE=AF,
∴EH=FH,
∵AH=GH,AG⊥EF,
∴四边形FGEA是菱形;
故④正确;
⑤设BG=x,则AF=AE=x,
由①知△BEG是等腰直角三角形,
∴BE=![]() x,
x,
∴AB=AE+BE=x+![]() x=(
x=(![]() +1)x,
+1)x,
∴AO=![]() =
=![]() ,
,
∴OF=AO﹣AF=![]() ﹣x=
﹣x=![]() x,
x,
∴![]() =
=![]() =
=![]() ,
,
∴OF=![]() BE;
BE;
故⑤正确;
本题正确的结论有:②③④⑤;
故选:C.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
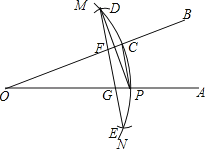
【题目】如图,∠AOB=20°,点P在OA边上.
(1)以点O为圆心,OP长为半径作![]() ,交OB于点C;
,交OB于点C;
(2)分别以点P、C为圆心,PC长为半径作弧,交![]() 于点D、E;
于点D、E;
(3)连接DE,分别交OC、OP于点F、G;
(4)连接DP.
根据以上作图过程及所作图形,下列结中正确的是_____.(填序号)
①OC垂直平分DP;②∠COD=∠COP;③DF=FG;④OD=DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
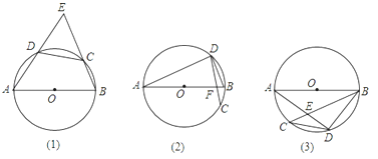
【题目】已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.
(1)∠E的度数为.
(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
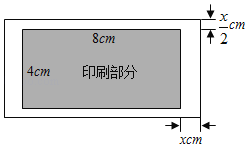
【题目】如图,印刷一张矩形的包装纸,印刷部分的长为8cm,宽为4cm,上下空白宽各![]() cm,左右空白宽各xcm,四周空白处的面积为Scm2.
cm,左右空白宽各xcm,四周空白处的面积为Scm2.
(1)求S与x的关系式;
(2)当四周空白处的面积为18cm2时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
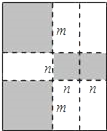
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)
(1)用含m,n的代数式表示所有裁剪线(图中虚线部分)的长度之和;
(2)观察图形,发现代数式2m2+5mn+2n2可以因式分解为 ;
(3)若每块小矩形的面积为10cm2,四个正方形的面积和为58cm2,试求(m+n)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com