
【题目】已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.
(1)∠E的度数为.
(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
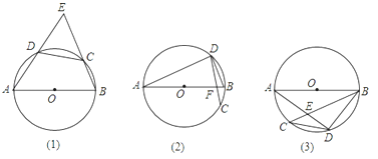
【答案】(1)60°(2)60°(3)60°
【解析】
(1)连结OD,OC,BD,根据已知得到△DOC为等边三角形,由圆周角定理可得∠DBC=30°,根据直径所对的圆周角是直角,求出∠E的度数即可;(2)根据已知可得△DOC为等边三角形,根据圆周角定理可得∠DAC=30°,由圆内接四边形性质可得∠EBD=∠DAC=30°,根据直径所对的圆周角是直角,求出∠E的度数即可;(3)根据已知可得△DOC为等边三角形,根据圆周角定理可知∠CAD=30°,根据直径所对的圆周角是直角,求出∠AEC的度数即可;
(1)如图1,连结OD,OC,BD,
∵OD=OC=CD=2
∴△DOC为等边三角形,
∴∠DOC=60°
∴∠DBC=30°
∴∠EBD=30°
∵AB为直径,
∴∠ADB=90°
∴∠E=90°﹣30°=60°.

(2)①如图2,直线AD,CB交于点E,连结OD,OC,AC,.
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠DAC=30°,
∵∠EBD是圆内接四边形ACBD的外角,
∴∠EBD=30°,
∵AB为直径,
∴∠ACB=90°,
∴∠E=90°﹣30°=60°,
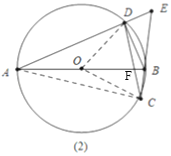
(3)如图3,连结OD,OC,AC,
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠CAD=30°,
∵AB是直径,∠ACB是AB所对的圆周角,
∴∠ACB=90°,
∴∠AEC=90°-30°=60°.


科目:初中数学 来源: 题型:
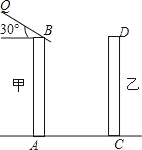
【题目】如图,是住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=30m,现需了解甲楼对乙楼的采光的影响情况.
(1)当太阳光与水平线的夹角为30°角时,求甲楼的影子在乙楼上有多高(精确到0.1m,![]() =1.73);
=1.73);
(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为边BC的中点,四边形ABDE是平行四边形,AC,DE相交于点O.
(1)求证:四边形ADCE是矩形;
(2)若∠AOE=60°,AE=2,求矩形ADCE对角线的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂要把一批产品从A地运往B地,若通过铁路运输,则每千米需交运费15元,还要交装卸费400元及手续费200元,若通过公路运输,则每千米需要交运费25元,还需交手续费100元(由于本厂职工装卸,不需交装卸费).设A地到B地的路程为x km,通过铁路运输和通过公路运输需交总运费y1元和y2元,
(1)求y1和y2关于x的表达式.
(2)若A地到B地的路程为120km,哪种运输可以节省总运费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(3a+2b)(3a-2b)-(3a-2b)2
(2)(a-5) 2-(a+6)(a-6)
(3)(3x-2y)2-(2x-y)(x-y)
(4)(-4a)·(2a2+3a-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC,BD交于点O,AG平分∠BAC交BD于G,DE⊥AG于点H.下列结论:①AD=2AE:②FD=AG;③CF=CD:④四边形FGEA是菱形;⑤OF=![]() BE,正确的有( )
BE,正确的有( )
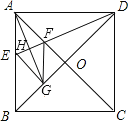
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.

依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com