
【题目】已知![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦.
的弦.
(1)如图①,连接![]() ,若
,若![]() ,求
,求![]() 的大小;
的大小;

(2)如图②;![]() 是半圆弧
是半圆弧![]() 的中点,
的中点,![]() 的延长线与过点
的延长线与过点![]() 的切线相交于点
的切线相交于点![]() ,若
,若![]() ,求
,求![]() 的大小.
的大小.
科目:初中数学 来源: 题型:
【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

查看答案和解析>>
科目:初中数学 来源: 题型:
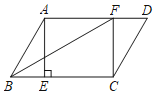
【题目】如图,ABCD中,点E,F分别在边BC,AD上,BE=DF,∠AEC=90°.
(1)求证:四边形AECF是矩形;
(2)连接BF,若AB=4,∠ABC=60°,BF平分∠ABC,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示.有下列结论:①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0;⑤(a+c)2<b2.其中,正确结论的个数是( )
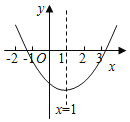
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
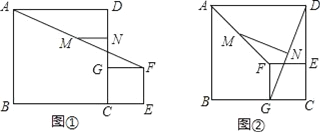
【题目】如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN
(1)线段MN和GD的数量关系是_____,位置关系是_____;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生参加社会实践活动情况,随机调查了本校部分八年级学生在第一学期参加社会实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
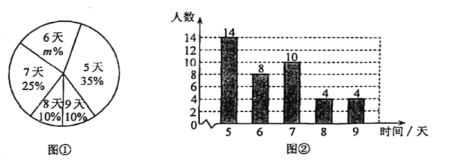
(1)本次接受随机抽样调查的学生人数为 ,图①中的![]() 的值为 ;
的值为 ;
(2)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(3)若该校八年级学生有![]() 人,估计参加社会实践活动时间大于
人,估计参加社会实践活动时间大于![]() 天的学生人数.
天的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
(1)请在图①的![]() 的边
的边![]() 上求作一点
上求作一点![]() ,使
,使![]() 最短;
最短;
(2)如图②,点![]() 为
为![]() 内部一点,且满足
内部一点,且满足![]() .求证:点
.求证:点![]() 到点
到点![]() 、
、![]() 、
、![]() 的距离之和最短,即
的距离之和最短,即![]() 最短;
最短;
问题解决
(3)如图③,某高校有一块边长为400米的正方形草坪![]() ,现准备在草坪内放置一对石凳及垃圾箱在
,现准备在草坪内放置一对石凳及垃圾箱在![]() 点处,使点
点处,使点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离之和最小,那么是否存在符合条件的点
三点的距离之和最小,那么是否存在符合条件的点![]() ?若存在,请作出点
?若存在,请作出点![]() 的位置,并求出这个最短距离;若不存在,请说明理由.
的位置,并求出这个最短距离;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com