
解:(1)∵y=ax
2-4ax+4a+c=a(x-2)
2+c,
∴抛物线的对称轴为直线x=2.
∵抛物线y=ax
2-4ax+4a+c与x轴交于点A、点B,点A的坐标为(1,0),
∴点B的坐标为(3,0),OB=3.
可得该抛物线的解析式为y=a(x-1)(x-3).
∵OB=OC,抛物线与y轴的正半轴交于点C,
∴OC=3,点C的坐标为(0,3).
将点C(0,3)代入该解析式y=a(x-1)(x-3).
解得a=1.
∴此抛物线的解析式为y=x
2-4x+3.(如图1)
(2)作△ABC的外接圆☉E,设抛物线的对称轴与x轴的交点为点F,设☉E与抛物线的对称轴位于x轴上方的部分的交点为点P
1,点P
1关于x轴的对称点为点P
2,点P
1、点P
2均为所求点.(如图2)
可知圆心E必在AB边的垂直平分线即抛物线的对称轴直线x=2上.
∵∠AP
1B、∠ACB都是弧AB所对的圆周角,
∴∠AP
1B=∠ACB,且射线FE上的其它点P都不满足∠APB=∠ACB.
由(1)可知∠OBC=45°,AB=2,OF=2.
可得圆心E也在BC边的垂直平分线即直线y=x上.
∴点E的坐标为E(2,2).
∴由勾股定理得 EA=

.
∴EP
1=EA=

.
∴点P
1的坐标为P
1(2,2+

).
由对称性得点P
2的坐标为P
2(2,-2-

).
∴符合题意的点P的坐标为P
1(2,2+

)、P
2(2,-2-

).

(3)∵点B、D的坐标分别为B(3,0)、D(2,-1),
可得直线BD的解析式为y=x-3,直线BD与x轴所夹的锐角为45°.
∵点A关于∠AQB的平分线的对称点为A',(如图3)
若设AA'与∠AQB的平分线的交点为M,
则有 QA=QA',AM=A'M,AA'⊥QM,Q,B,A'三点在一条直线上.
∵QA-QB=

,
∴BA'=QA'-QB=QA-QB=

.
作A'N⊥x轴于点N.
∵点Q在线段BD上,Q,B,A'三点在一条直线上,
∴A'N=BA'•sin45°=1,BN=BA'•cos45°=1.
∴点A'的坐标为A'(4,1).
∵点Q在线段BD上,
∴设点Q的坐标为Q(x,x-3),其中2<x<3.
∵QA=QA',
∴由两点间的距离公式得 (x-1)
2+(x-3)
2=(x-4)
2+(x-3-1)
2.
解得x=

.
经检验,x=

在2<x<3的范围内.
∴点Q的坐标为Q(

,-

).
此时S
△QAA'=S
△A'AB+S
△QAB=

•AB•(|y
A'|+|y
Q|)=

×2×(1+

)=

.
分析:(1)首先将已知的抛物线解析式进行配方,得出对称轴方程后结合A点坐标可确定B点的坐标,由OB=OC的条件能得到C点坐标,利用待定系数法即可确定函数的解析式.
(2)此题需要进行适当转化,首先作△ABC的外切圆,根据圆周角定理可知:P点应为抛物线对称轴与⊙E的交点(相关字母参考解答图,下同),那么只需求出圆心E的坐标和⊙E的半径即可得到P点坐标.首先由A、B的坐标可确定F点的坐标以及AF的长,而弦BC的垂直平分线过点E,由此可确定该中垂线的解析式,进一步可确定点E的坐标;然后在Rt△AEF中,通过解直角三角形可得到圆的半径长,由此求出全部条件.
(3)A、A′关于角平分线对称,那么QA、QA′也关于该角平分线对称,即QA=QA′,那么QA-QB的长其实就是AB的长,可由这个条件入手解答;易知点D、B的坐标,能求出∠ABD的度数(或相关三角函数值),过A′作A′N⊥x轴,在构建的Rt△A′BN中,∠A′BN的度数已求出,可得到BN、A′N的长,即可求出A′的坐标和直线A′B的解析式,然后设出点Q坐标,表示出AQ、A′Q的长,以这两条线段相等作为等量条件求出点Q的坐标.进一步以AB为底、点A′、Q的纵坐标的差的绝对值为高可求出△AQA′的面积.
点评:这道二次函数题由于融合了圆、解直角三角形、轴对称图形等重点知识,使得难度增加不少;(2)题中,将角相等转化为圆的相关问题是打开解题突破口的关键,应注意并总结转化思想在解题中的妙用.

 ,求点Q的坐标和此时△QAA′的面积.
,求点Q的坐标和此时△QAA′的面积.
 解:(1)∵y=ax2-4ax+4a+c=a(x-2)2+c,
解:(1)∵y=ax2-4ax+4a+c=a(x-2)2+c, .
. .
. ).
). ).
).  )、P2(2,-2-
)、P2(2,-2- ).
). (3)∵点B、D的坐标分别为B(3,0)、D(2,-1),
(3)∵点B、D的坐标分别为B(3,0)、D(2,-1), ,
, .
. .
. 在2<x<3的范围内.
在2<x<3的范围内. ,-
,- ).
).  •AB•(|yA'|+|yQ|)=
•AB•(|yA'|+|yQ|)= ×2×(1+
×2×(1+ )=
)= .
.

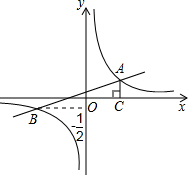 如图,已知在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,已知在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=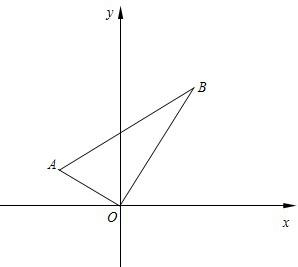 90°,∠A=60°,点A的坐标为(-
90°,∠A=60°,点A的坐标为(-
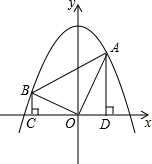 A,OB,OA⊥OB,作BC⊥x轴于C点,AD⊥x轴于D点.
A,OB,OA⊥OB,作BC⊥x轴于C点,AD⊥x轴于D点.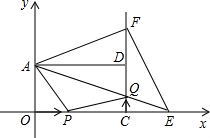 (2013•河东区一模)如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P、Q同时出发,同时停止,设运动时间为t秒,当t=2秒时PQ=2
(2013•河东区一模)如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P、Q同时出发,同时停止,设运动时间为t秒,当t=2秒时PQ=2