
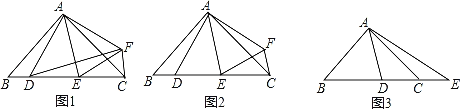
【题目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)成立,理由见解析.
【解析】试题分析:(1)根据轴对称的性质可得∠EAF=∠DAE,AD=AF,再求出∠BAC=∠DAF,然后根据两边对应成比例,夹角相等两三角形相似证明;
(2)根据轴对称的性质可得EF=DE,AF=AD,再求出∠BAD=∠CAF,然后利用“边角边”证明△ABD和△ACF全等,根据全等三角形对应边相等可得CF=BD,全等三角形对应角相等可得∠ACF=∠B,然后求出∠ECF=90°,最后利用勾股定理证明即可;
(3)作点D关于AE的对称点F,连接EF、CF,根据轴对称的性质可得EF=DE,AF=AD,再根据同角的余角相等求出∠BAD=∠CAF,然后利用“边角边”证明△ABD和△ACF全等,根据全等三角形对应边相等可得CF=BD,全等三角形对应角相等可得∠ACF=∠B,然后求出∠ECF=90°,最后利用勾股定理证明即可.
试题解析:(1)∵点D关于直线AE的对称点为F,
∴∠EAF=∠DAE,AD=AF,
又∵∠BAC=2∠DAE,
∴∠BAC=∠DAF,
∵AB=AC,
∴![]() ,
,
∴△ADF∽△ABC;
(2)∵点D关于直线AE的对称点为F,
∴EF=DE,AF=AD,
∵α=45°,
∴∠BAD=90°﹣∠CAD,
∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD,
∴∠BAD=∠CAF,
在△ABD和△ACF中,

∴△ABD≌△ACF(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=2α,α=45°,
∴△ABC是等腰直角三角形,
∴∠B=∠ACB=45°,
∴∠ECF=∠ACB+∠ACF=45°+45°=90°,
在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,
所以,DE2=BD2+CE2;
(3)DE2=BD2+CE2还能成立.
理由如下:作点D关于AE的对称点F,连接EF、CF,

由轴对称的性质得,EF=DE,AF=AD,
∵α=45°,
∴∠BAD=90°﹣∠CAD,
∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD,
∴∠BAD=∠CAF,
由(2)得:CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=2α,α=45°,
∴△ABC是等腰直角三角形,
∴∠B=∠ACB=45°,
∴∠ECF=∠ACB+∠ACF=45°+45°=90°,
在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,
所以,DE2=BD2+CE2.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
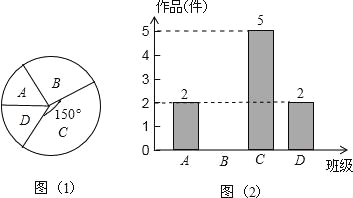
【题目】我市某中学艺术节期间,向全校学生征集书画作品.九年级美术王老师从全年级14个班中随机抽取了4个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
(1)王老师采取的调查方式是 (填“普查”或“抽样调查”),王老师所调查的4个班征集到作品共 件,其中b班征集到作品 件,请把图2补充完整;
(2)王老师所调查的四个班平均每个班征集作品多少件?请估计全年级共征集到作品多少件?
(3)如果全年级参展作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生.现在要在其中抽两人去参加学校总结表彰座谈会,请直接写出恰好抽中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某反比例函数的图象经过点A(﹣3,6),则下列各点中不在此函数图象上的是( )
A. (3,﹣6) B. (6,3) C. (﹣2,9) D. (﹣9,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育局为了解该市2006年九年级学生的身体素质情况,随机抽取了1000名九年级学生进行检测,身体素质达标率为95%,请你估计该市12万名九年级学生中,身体素质达标的大约有_____万人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于函数 y=3-x,下列结论正确的是( )
A.y 的值随 x 的增大而增大B.它的图象必经过点(-1,3)
C.它的图象不经过第三象限D.当 x>1 时,y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3)+(﹣4)﹣(+11)﹣(﹣19)
(2)﹣10﹣8÷(﹣2)×(﹣![]() )
)
(3)(![]() ﹣
﹣![]() )×30÷(﹣
)×30÷(﹣![]() )
)
(4)(﹣![]() +
+![]() ﹣
﹣![]() )×|﹣12|
)×|﹣12|
(5)18×![]() +13×
+13×![]() ﹣4×
﹣4×![]() .
.
(6)(﹣36![]() )÷9.
)÷9.
查看答案和解析>>
科目:初中数学 来源: 题型:
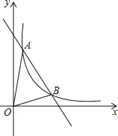
【题目】如图,一次函数y=kx+b与反比例函数![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b-![]() <0的x的取值范围;
<0的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地球上的海洋面积约为361 000 000平方千米,数字361 000 000用科学记数法表示为( )
A. 36.1×107 B. 0.36×109
C. 3.61×108 D. 3.61×107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com