
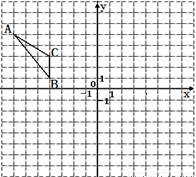
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a﹣b=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确有( )个。
A.2个 B.3个 C.4个 D.5个

B .
【解析】
试题分析:①由图知:抛物线与x轴有两个不同的交点,则△=b2-4ac>0,∴b2>4ac,故①正确;
②抛物线开口向上,得:a>0;
抛物线的对称轴为x=-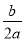 =1,b=-2a,故b<0;
=1,b=-2a,故b<0;
抛物线交y轴于负半轴,得:c<0;
所以abc>0;
故②正确;
③∵抛物线的对称轴为x=-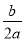 =1,b=-2a,
=1,b=-2a,
∴2a+b=0,故2a-b=0错误;
④根据②可将抛物线的解析式化为:y=ax2-2ax+c(a≠0);
由函数的图象知:当x=-2时,y>0;即4a-(-4a)+c=8a+c>0,故④错误;
⑤根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故⑤正确;
所以这结论正确的有①②⑤.
故选B.
考点:二次函数图象与系数的关系.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源:2014中考名师推荐数学一元一次不等式组(解析版) 题型:填空题
按如下程序进行运算:
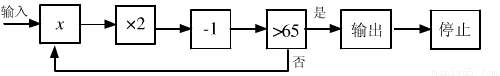
并规定:程序运行到“结果是否大于65”为一次运算,且运算进行4次才停止,则可输入的整数x的个数是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题四数学试卷(解析版) 题型:解答题
如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(1)求证:DP平分∠ADC;
(2)若∠CEF=75°,CF= ,求△AEF的面积.
,求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题四数学试卷(解析版) 题型:填空题
小明动手做了一个质地均匀、六个面完全相同的正方体,,分别标有整数-2、-1、0、1、2、3,且每个面和它所相对的面的数字之和均相等,小明向上抛掷该正方体,落地后正方体正面朝上数字作为为点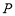 的横坐标,将它所对的面的数字作为点
的横坐标,将它所对的面的数字作为点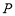 的纵坐标,则点
的纵坐标,则点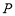 落在抛物线
落在抛物线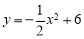 与
与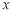 轴所围成的区域内(不含边界)的概率是 .
轴所围成的区域内(不含边界)的概率是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题四数学试卷(解析版) 题型:选择题
下列事件是随机事件的是 ( )
A.购买一张福利彩票,中特等奖
B.在一个标准大气压下,将水加热到100℃,水沸腾
C.奥林匹克运动会上,一名运动员奔跑的速度是30米/秒
D.在一个只装着白球和黑球的袋中摸球,摸出一个红球
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题二数学试卷(解析版) 题型:解答题
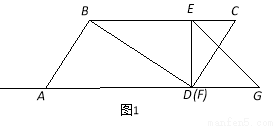
如图1,□ABCD中,对角线BD⊥AB,AB=5,AD边上的高为 .等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t.
.等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t.
(1)求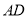 的长度;
的长度;
(2)在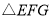 平移的过程中,记
平移的过程中,记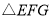 与
与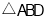 相互重叠的面积为
相互重叠的面积为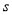 ,请直接写出面积
,请直接写出面积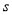 与运动时间
与运动时间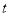 的函数关系式,并写出
的函数关系式,并写出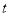 的取值范围;
的取值范围;
(3)如图2,在运动的过程中,若线段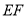 与线段
与线段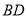 交于点
交于点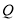 ,连接
,连接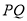 .是否存在这样的时间
.是否存在这样的时间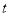 ,使得
,使得 为等腰三角形?若存在,求出对应的
为等腰三角形?若存在,求出对应的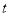 值;若不存在,请说明理由.
值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题二数学试卷(解析版) 题型:选择题
下列各图形都是由同样大小的圆和正三角形按一定的规律组成.其中,第①个图形由8个圆和1个正三角形组成,第②个图形由16个圆和4个正三角形组成,第③个图形由24个圆和9个正三角形组成,……则第几个图形中圆和正三角形的个数相等.( ) .

A.7 B.8 C.9 D.10
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级3月月考数学试卷(解析版) 题型:解答题
如图所示,△ABC在平面直角坐标系中,将△ABC向下平移5个单位得到△A1B1C1,再将△A1B1C1绕点o顺时针旋转90°得到△A2B2C2,请作出△A1B1C1和△A2B2C2;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com