练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    先化简，再求值：
    3-x
    x-2
    ÷[（x+2）-
    5
    x-2
    ]，其中x=1．
    考点：分式的化简求值
    专题：
    分析：先根据分式混合运算的法则把原式进行化简，再把x=1代入进行计算即可．
    解答：解：原式=
    3-x
    x-2
    ÷
    x2-4-5
    x-2

    =
    3-x
    x-2
    •
    x-2
    (x-3)(x+3)

    =-
    1
    x+3
    ，
    当x=1时，原式=-
    1
    1+3
    =-
    1
    4
    ．
    点评：本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

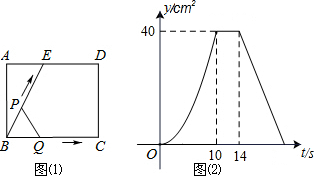    如图（1），E为矩形ABCD边AD上一点，点P从点B沿折线BE-ED-DC运动到点C时停止，点Q从点B沿BC运动到点C时停止，它们运动的速度都是1cm/s．如果点P、Q同时开始运动，设运动时间为t（s），△BPQ的面积为y（cm2），已知y与t的函数关系的图象如图（2）所示，那么下列结论正确的是（　　）
    A、AE=8
    B、当0≤t≤10时，y=
    2
    5
    t2
    C、sin∠EBD=
    4
    5
    D、当t=12s时，△BPQ是等腰三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

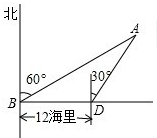    海岛A的周围8海里内有暗礁，渔船跟踪鱼群由西向东航行，在点B处测得海岛A位于北偏东60°，航行12海里后到达点D处，又测得海岛A位于北偏东30°，如果渔船不改变航向继续向东航行．有没有触礁的危险？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

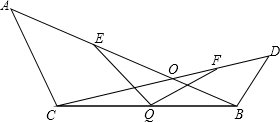    如图，已知：AB、CD交于点O，CA=CO，BO=BD，点Q是BC的中点，点E，F分别是OA，OD的中点，连接QE、QF，试探讨QE、QF的大小关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

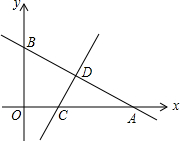    如图，一次函数y=kx+n的图象与x轴和y轴分别交于点A（6，0）和B（0，2
    		3
    ），线段AB的垂直平分线交x轴于点C，交AB于点D．
    （1）试确定这个一次函数解析式；
    （2）求过A、B、C三点的抛物线的函数关系式；
    （3）请你利用所求抛物线的图象回答：当x取何值时，抛物线中的部分图象落在x轴的上方？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如果有一列数，从这列数的第2个数开始，每一个数与它的前一个数的比等于同一个非零的常数，这样的一列数就叫做等比数列（Geometric Sequences）．这个常数叫做等比数列的公比，通常用字母q表示（q≠0）．
    （1）观察一个等比列数1，
    1
    2
    ，
    1
    4
    ，
    1
    8
    ，
    1
    16
    ，…，它的公比q=
     
    ；如果an（n为正整数）表示这个等比数列的第n项，那么a18=
     
    ，an=
     
    ；
    （2）如果欲求1+2+4+8+16+…+230的值，可以按照如下步骤进行：
    令S=1+2+4+8+16+…+230…①
    等式两边同时乘以2，得2S=2+4+8+16++32+…+231…②
    由②式减去①式，得2S-S=231-1
    即（2-1）S=231-1
    所以 S=
    231-1
    2-1
    =231-1
    请根据以上的解答过程，求3+32+33+…+323的值；
    （3）用由特殊到一般的方法探索：若数列a1，a2，a3，…，an，从第二项开始每一项与前一项之比的常数为q，请用含a1，q，n的代数式表示an；如果这个常数q≠1，请用含a1，q，n的代数式表示a1+a2+a3+…+an．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解下列不等式（组），并把它们的解集在数轴上表示出来：
    （1）5x+20≥0；
    （2）2（x-2）≤x-2；
    （3）
    x-1
    2
    +1≥x    ；
    （4）
    x
    3
    -1＜0
    x
    2
    +1＞
    x
    3
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

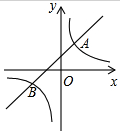     如图，直线y=x+2与双曲线y=
    k
    x
    （k≠0）相交于A（1，m），B（n，-1）两点．
    （1）求双曲线的解析式；
    （2）若C（a，p）为第一象限内双曲线上（除点A外）一点，请直接写出m，n，p的大小关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若关于x的方程
    x-2
    x-4
    =
    3
    x-4
    +m无解，则m=
     
    ．

    查看答案和解析>>

    同步练习册答案