
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D. 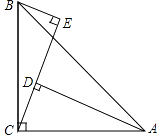
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
科目:初中数学 来源: 题型:
【题目】如图,若∠B=40°,A、C分别为角两边上的任意一点,连接AC,∠BAC与∠ACB的平分线交于点P1 , 则∠P1= , D、F也为角两边上的任意一点,连接DF,∠BFD与∠FDB的平分线交于点P2 , …按这样规律,则∠P2016= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某新型感冒病毒的直径约为0.000000823米,将0.000000823用科学记数法表示为( )
A. 8.23×10﹣6 B. 8.23×10﹣7 C. 8.23×106 D. 8.23×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交车原坐有22人,经过4个站点时上下车情况如下(上车为正,下车为负):(+4,﹣8),(﹣5,+6),(﹣3,+2),(+1,﹣7),则车上还有人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com