
 如图,已知:在△ABC中,∠ABC的平分线与AC边的垂直平分线相交于点N,过点N作ND⊥AB于D,NE⊥BC于E.求证:AD=CE.
如图,已知:在△ABC中,∠ABC的平分线与AC边的垂直平分线相交于点N,过点N作ND⊥AB于D,NE⊥BC于E.求证:AD=CE. 分析 连接AN、CN,根据线段垂直平分线的性质,得AN=CN,根据角平分线的性质,得DN=EN,再根据HL即可证明Rt△AND≌Rt△CNE,得出结论即可.
解答 证明:连接AN、CN.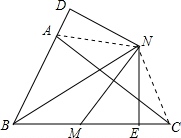
∵MN是AC边的垂直平分线,BN是∠ABC的平分线,ND⊥AB,NE⊥BC,
∴AN=CN,DN=EN,
在Rt△AND和Rt△CNE中,
$\left\{\begin{array}{l}{AN=CN}\\{DN=EN}\end{array}\right.$,
∴Rt△AND≌Rt△CNE,
∴AD=CE.
点评 此题考查全等三角形的判定和性质,线段垂直平分线的性质、角平分线的性质,结合图形,作出辅助线,找出全等的三角形是解决问题的关键.


科目:初中数学 来源: 题型:选择题
 如图,某酒店大门的旋转门内部由三块宽为2米,高为3米的玻璃隔板组成,三块玻璃摆放时夹角相同.若入口处两根立柱之间的距离为2米,则两立柱底端中点到中央转轴底端的距离为( )
如图,某酒店大门的旋转门内部由三块宽为2米,高为3米的玻璃隔板组成,三块玻璃摆放时夹角相同.若入口处两根立柱之间的距离为2米,则两立柱底端中点到中央转轴底端的距离为( )| A. | $\sqrt{3}$米 | B. | 2米 | C. | 2$\sqrt{2}$米 | D. | 3米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
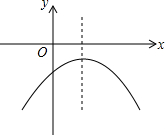 抛物线y=ax2+bx+c的图象如图所示,则( )
抛物线y=ax2+bx+c的图象如图所示,则( )| A. | a<0,△<0,b>0 | B. | a<0,△>0,b>0 | C. | a<0,△<0,b<0 | D. | a<0,△>0,b<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
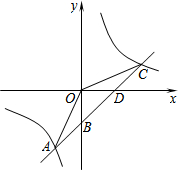 如图,一次函数y=kx+b的图象与反比例函数$y=\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
如图,一次函数y=kx+b的图象与反比例函数$y=\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com