练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．计算：$\frac{1}{a（a+1）}$+$\frac{1}{（a+1）（a+2）}$+$\frac{1}{（a+2）（a+3）}$+…+$\frac{1}{（a+2013）（a+2014）}$．

    分析 原式利用拆项法变形后，抵消合并即可得到结果．

    解答 解：原式=$\frac{1}{a}$-$\frac{1}{a+1}$+$\frac{1}{a+1}$-$\frac{1}{a+2}$+$\frac{1}{a+2}$-$\frac{1}{a+3}$+…+$\frac{1}{a+2013}$-$\frac{1}{a+2014}$=$\frac{1}{a}$-$\frac{1}{a+2014}$=$\frac{2014}{a（a+2014）}$．

    点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．一只不透明的箱子里共有8个球，其中2个白球，1个红球，5个黄球，它们除颜色外均相同．
    （1）从箱子中随机摸出一个球是白球的概率是多少？
    （2）再往箱子中放入黄球多少个，可以使摸到白球的概率达到0.2？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．阅读理解
    如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重叠部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重叠部分；…将余下部分沿∠BnAnC的平分线AnBn+1折叠，点Bn与点C重合．无论折叠多少次，只要最后一次恰好重合，我们就称∠BAC是△ABC的好角．

    小丽展示了确定∠BAC是△ABC的好角的两种情形．情形一：如图2，沿等腰三角形ABC顶角∠BAC是平分线AB1折叠，则等腰三角形的两个点B与点C重合（因为等腰三角形的两个底角是相等的）；情形二：如图3，沿△ABC的∠BAC的平分线AB1折叠，剪掉重叠部分；将余下的部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合．
    探究发现
    （1）△ABC中，∠B=2∠C，经过两次折叠，∠BAC是不是△ABC的好角？是（填“是”或“不是”）
    （2）小丽经过三次折叠发现了∠BAC是△ABC的好角，请探究∠B与∠C（不妨设∠B＞∠C）之间的等量关系，写出探究过程．
    根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系是∠B=n∠C．．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．解方程：3x2-2x-1=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．计算：（-$\frac{1}{2}$a3b）2•b2=$\frac{1}{4}$a6b4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：（$\sqrt{a}$+$\sqrt{b}$+1）（$\sqrt{b}$+1-$\sqrt{a}$）-（$\sqrt{a}$+$\sqrt{b}$）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

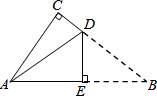    8．如图是一张直角三角形的纸片，两直角边AC=6cm、BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为（　　）
    A．4cmB．5cmC．6cmD．10cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．路人甲从A地走往B地要40分钟，路人乙从B地走往A地需30分钟，两人同时从AB两地出发，相遇时路人甲走了416米，A，B两地相距多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

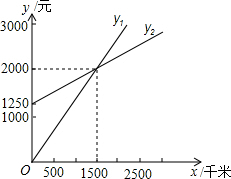    12．某单位准备租用一辆汽车，设汽车每月行驶x km，甲，乙两个出租车公司的月收费分别为y1元和y2元，y1，y2与x之间的函数关系图象如图，观察图象回答下列问题：
    （1）x在什么范围时，租甲公司车合算？
    （2）x在什么范围时，租乙公司车合算？
    （3）如果一个月这辆车行驶了3000km，这个单位最低应付多少元车费？

    查看答案和解析>>

    同步练习册答案