
【题目】已知双曲线y=![]() (x>0),直线l1:y﹣
(x>0),直线l1:y﹣![]() =k(x﹣
=k(x﹣![]() )(k<0)过定点F且与双曲线交于A,B两点,设A(x1 , y1),B(x2 , y2)(x1<x2),直线l2:y=﹣x+
)(k<0)过定点F且与双曲线交于A,B两点,设A(x1 , y1),B(x2 , y2)(x1<x2),直线l2:y=﹣x+![]() .
.
(1)若k=﹣1,求△OAB的面积S;
(2)
若AB=![]() , 求k的值;
, 求k的值;
(3)设N(0,2![]() ),P在双曲线上,M在直线l2上且PM∥x轴,求PM+PN最小值,并求PM+PN取得最小值时P的坐标.
),P在双曲线上,M在直线l2上且PM∥x轴,求PM+PN最小值,并求PM+PN取得最小值时P的坐标.
(参考公式:在平面直角坐标系中,若A(x1 , y1),B(x2 , y2)则A,B两点间的距离为AB=![]() )
)
【答案】
(1)
解:当k=-1时,l1:y=﹣x+2![]() ,
,
联立得,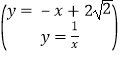 ,化简得x2﹣2
,化简得x2﹣2![]() x+1=0,
x+1=0,
解得:x1=![]() ﹣1,x2=
﹣1,x2=![]() +1,
+1,
设直线l1与y轴交于点C,则C(0,2![]() ).
).
S△OAB=S△AOC﹣S△BOC=![]() 2
2![]() (x2﹣x1)=2
(x2﹣x1)=2![]() ;
;
(2)
解:根据题意得: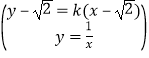 整理得:kx2+
整理得:kx2+![]() (1﹣k)x﹣1=0(k<0),
(1﹣k)x﹣1=0(k<0),
∵△=[![]() (1﹣k)]2﹣4×k×(﹣1)=2(1+k2)>0,
(1﹣k)]2﹣4×k×(﹣1)=2(1+k2)>0,
∴x1、x2 是方程的两根,
∴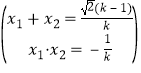 ①,
①,
∴AB=![]() =
=![]()
=![]()
=![]() ,
,
将①代入得,AB=![]() =
=![]() (k<0),
(k<0),
∴![]() =
=![]() ,
,
整理得:2k2+5k+2=0,
解得:k=﹣2,或 k=![]() ;
;
(3)
解:∵直线l1:y﹣![]() =k(x﹣
=k(x﹣![]() )(k<0)过定点F,
)(k<0)过定点F,
∴ F(![]() ,
,![]() ).
).
如图:
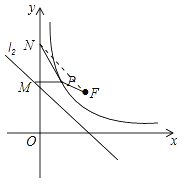
设P(x,![]() ),则M(﹣
),则M(﹣![]() +
+![]() ,
,![]() ),
),
则PM=x+![]() ﹣
﹣![]() =
=![]() =
=![]() ,
,
∵PF=![]() =
=![]() ,
,
∴PM=PF.
∴PM+PN=PF+PN≥NF=2,
当点P在NF上时等号成立,此时NF的方程为y=﹣x+2![]() ,
,
由(1)知P(![]() ﹣1,
﹣1,![]() +1),
+1),
∴当P(![]() ﹣1,
﹣1,![]() +1)时,PM+PN最小值是2.
+1)时,PM+PN最小值是2.
【解析】(1)将l1与y=![]() 组成方程组,即可得到C点坐标,从而求出△OAB的面积;
组成方程组,即可得到C点坐标,从而求出△OAB的面积;
(2)根据题意得: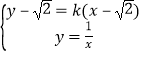 整理得:kx2+
整理得:kx2+![]() (1﹣k)x﹣1=0(k<0),根据根与系数的关系得到2k2+5k+2=0,从而求出k的值;
(1﹣k)x﹣1=0(k<0),根据根与系数的关系得到2k2+5k+2=0,从而求出k的值;
(3)设P(x,![]() ),则M(﹣
),则M(﹣![]() +
+![]() ,
, ![]() ),根据PM=PF,求出点P的坐标.
),根据PM=PF,求出点P的坐标.


科目:初中数学 来源: 题型:
【题目】如图,△ABE是⊙O的内接三角形,AB为直径,过点B的切线与AE的延长线交于点C,D是BC的中点,连接DE,连接CO,线段CO的延长线交⊙O于F,FG⊥AB于G. 
(1)求证:DE是⊙O的切线;
(2)若AE=4,BE=2,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲经销商库存有1200套A品牌服装,每套进价400元,每套售价500元,一年内可卖完,现市场流行B品牌服装,每套进价300元,每套售价600元,但一年内只允许经销商一次性订购B品牌服装,一年内B品牌服装销售无积压,因甲经销商无流动资金可用,只有低价转让A品牌服装,用转让来的资金购进B品牌服装,并销售,经与乙经销商协商,甲、乙双方达成转让协议,转让价格y(元/套)与转让数量x(套)之间的函数关系式为y=﹣![]() x+360(100≤x≤1200),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).
x+360(100≤x≤1200),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).
(1)求转让后剩余的A品牌服装的销售款Q1(元)与x(套)之间的函数关系式;
(2)求B品牌服装的销售款Q2(元)与x(套)之间的函数关系式;
(3)求W(元)与x(套)之间的函数关系式,并求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.
(1)求BC的长;
(2)过点D作DE⊥AC,垂足为E,求证:直线DE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】质地均匀的小正方体,六个面分别有数字“1”、“2”、“3”、“4”、“5”、“6”,同时投掷两枚,观察朝上一面的数字.
(1)求数字“1”出现的概率;
(2)求两个数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一次函数y=﹣2x+10的图象与反比例函数![]() (k>0)的图象相交于A,B两点(A在B的右侧).
(k>0)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在1的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com