
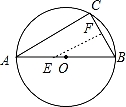
如图,AB是⊙O的直径,弦BC=4cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A的方向运动,设运动时间为t(s)(0≤t<6),连接EF,当△BEF是直角三角形时,t的值为 .
2,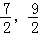 .
.
【考点】圆周角定理;含30度角的直角三角形;勾股定理;垂径定理.
【专题】压轴题.
【分析】求出E移动的路程是0≤s <12,求出∠C=90°,求出AB,分为三种情况:画出图形,根据图形求出移动的距离即可.
<12,求出∠C=90°,求出AB,分为三种情况:画出图形,根据图形求出移动的距离即可.
【解答】解:∵0≤t<6,动点E以2cm/s的速度从A点出发沿着A→B→A的方向运动,
∴当t=6时,运动的路程是2×6=12(cm),
即E运动的距离小于12cm,设E运动的距离是scm,
则0≤s<12,
∵AB是⊙O直径,
∴∠C=90°,
∵F为BC中点,BC=4cm,
∴BF=CF=2cm,
∵∠C=90°,∠B=60°,
∴∠A=30°,
∴AB=2BC=8cm,
分为三种情况:
①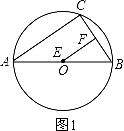
当∠EFB=90°时,
∵∠C=90°,
∴∠EFB=∠C,
∴AC∥EF,
∵FC=BF,
∴AE=BE,即E和O重合,AE=4,
t=4÷2=2(s);
②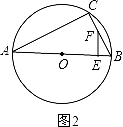
当∠FEB=90°时,∵∠ABC=60°,
∴∠BFE=30°,
∴BE= BF=1,
BF=1,
AE=8﹣1=7,
t=7÷2=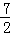 (s);
(s);
③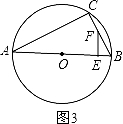
当到达B后再返回到E时,∠FEB=90°,
此时移动的距离是8+1=9,
t=9÷2=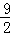 (s);
(s);
故答案为:2,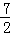 ,
,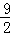 .
.
【点评】本题考查了圆周角定理,含30度角的直角三角形性质,平行线分线段成比例定理等知识点的综合运用,注意要进行分类讨论啊.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
在△ABC中,∠C=90O,BC=8cm,∠BAC的平分线交BC于点 D,且BD:DC=5:3,则点D到AB的距离为( )
D,且BD:DC=5:3,则点D到AB的距离为( )
A. 2 cm B. 3 cm C. 5 cm D. 8 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法中正确的是( )
A.“任意画出一个等边三角形,它是轴对称图形”是随机事件
B.“任意画出一个平行四边形,它是中心对称图形”是必然事件
C.“概率为0.0001的事件”是不可能 事件
事件
D.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的方程x2+2x+a﹣2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)当该方程的一个根为1时,求a的值及方程的另一根.
查看答案和解析>>
科目:初中数学 来源: 题型:
某超市在元旦节期间实行让利销售,全部商品一律按九折销售,这样每天所获 得的利润恰是销售收入的20%,如果笫一天的销售收入为4万元,且每天的销售收入都有增长.笫三天的利润是0.968万元.
得的利润恰是销售收入的20%,如果笫一天的销售收入为4万元,且每天的销售收入都有增长.笫三天的利润是0.968万元.
(1)求第三天的销售收入是多少万元?
(2)第二天和第三天销售收入平均每天增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
| x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com