如图，把Rt△ABC绕点A逆
时针旋转40°，得到Rt△AB′C′，点C′恰好落在边AB上，连接BB′，则∠BB′C′= 度．
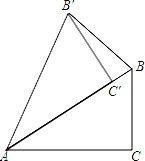
20 度．
【考点】旋转的性质．
【专题】计算题．
【分析】先根据旋转的性质得到∠ACB′=∠C=90°，∠BAB′=40°，AB=AB′，则利用等腰三角形的性质和三角形内角和定理可计算出∠ABB′=70°，然后利用互余计算∠BB′C′．
【解答】解：∵Rt△ABC绕点A逆时针旋转40°，得到Rt△AB′C′，点C′恰好落在边AB上，
∴∠ACB′=∠C=90°，∠BAB′=40°，AB=AB′，
∵AB=AB′，
∴∠ABB′=∠AB′B，
∴∠ABB′=
（180°﹣40°）=70°，
∴∠BB′C′=90°﹣∠CBB′=20°．
故答案为20．
【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．
科目：初中数学 来源： 题型：
.用电脑程序控制小型赛车进行50m比赛，“畅想号”和“和谐号”两赛车进入了决赛，比赛前的练习中，两辆车从起点同时出发，“畅想号”到达终点时，“和谐号”离终点还差3m，已知“畅想号”的平均速度为2.5m/s
（1）求“和谐号”的平均速度;
（2）如果两车重新开始比赛，“畅想号”从起点向后退3m ，两车 同时出发，两车能否同时到达终点？若能，求出两车到达终点的时间;若不能，请重新调整一辆车的平均速度，使两车能同时到达终点。
查看答案和解析>>
科目：初中数学 来源： 题型：
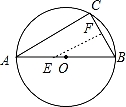
如图，AB是⊙O的直径，弦BC=4cm，F是弦BC的中点，∠ABC=60°．若动点E以2cm/s的速度从A点出发沿着A→B→A的方向运动，设运动时间为t（s）（0≤t＜6），连接EF，当△BEF是直角三角形时，t的值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
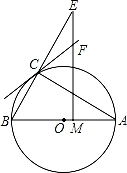
如图，⊙O是△ABC的外接圆，圆心O在AB上，且∠B=2∠A，M是OA上一点，过M作AB的垂线交AC于点N，交BC的延长线于点E，直线CF交EN于点F，EF=FC．
（1）求证：CF是⊙O的切线．
（2）设⊙O的半径为2，且AC=CE，求AM的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
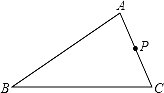
如图所示，在△ABC中，AB=6，AC=4，P是AC的中点，过P点的直线交AB于点Q，若以A、P、Q为顶点的三角形和以A、B、C为顶点的三角形相似，则AQ的长为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
是AC的中点．若AD=6，DE=5，则CD的长等于 ．
a3 C. (a2)3=a6 D. 2a+3a2=5a3 
的中点，∠ABC=50°，则∠DAB等于（ ）
